Динамичното програмиране е техника, която разделя проблемите на подпроблеми и запазва резултата за бъдещи цели, така че да не се налага да изчисляваме резултата отново. Подпроблемите са оптимизирани за оптимизиране на цялостното решение, което е известно като оптимално свойство на подструктура. Основната употреба на динамичното програмиране е за решаване на проблеми с оптимизацията. Тук оптимизационните проблеми означават, че когато се опитваме да намерим минималното или максималното решение на даден проблем. Динамичното програмиране гарантира намирането на оптималното решение на проблем, ако то съществува.

Дефиницията на динамичното програмиране гласи, че това е техника за решаване на сложен проблем, като първо се разбие колекция от по-прости подпроблеми, решавайки всеки подпроблем само веднъж и след това съхранявайки решенията им, за да избегнете повтарящи се изчисления.

Нека разберем този подход чрез пример.

Помислете за пример за редицата на Фибоначи. Следната серия е серия на Фибоначи:

как да дереферирам указател в c

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,…

Числата в горните серии не са изчислени на случаен принцип. Математически бихме могли да напишем всеки от термините, използвайки формулата по-долу:

F(n) = F(n-1) + F(n-2),

С базовите стойности F(0) = 0 и F(1) = 1. За да изчислим другите числа, следваме горната зависимост. Например F(2) е сумата f(0) и f(1), което е равно на 1.

Как можем да изчислим F(20)?

Членът F(20) ще бъде изчислен с помощта на n-тата формула от редицата на Фибоначи. Фигурата по-долу показва как се изчислява F(20).

хвърляне на обработка на изключения в Java

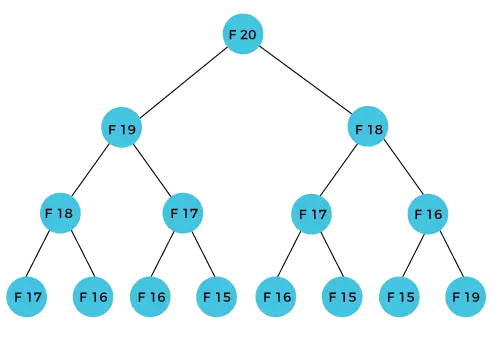
Както можем да видим на фигурата по-горе, F(20) се изчислява като сбор от F(19) и F(18). В подхода на динамичното програмиране се опитваме да разделим проблема на подобни подпроблеми. Ние следваме този подход в горния случай, където F(20) в подобни подпроблеми, т.е. F(19) и F(18). Ако обобщим дефиницията на динамичното програмиране, тя казва, че подобен подпроблем не трябва да се изчислява повече от веднъж. Все пак в горния случай подпроблемът се изчислява два пъти. В горния пример F(18) се изчислява два пъти; по подобен начин F(17) също се изчислява два пъти. Въпреки това, тази техника е доста полезна, тъй като решава подобни подпроблеми, но трябва да бъдем внимателни, докато съхраняваме резултатите, защото не сме специални за съхраняването на резултата, който сме изчислили веднъж, тогава това може да доведе до загуба на ресурси.

В горния пример, ако изчислим F(18) в дясното поддърво, това води до огромно използване на ресурси и намалява цялостната производителност.

Решението на горния проблем е да запишете изчислените резултати в масив. Първо изчисляваме F(16) и F(17) и запазваме стойностите им в масив. F(18) се изчислява чрез сумиране на стойностите на F(17) и F(16), които вече са записани в масив. Изчислената стойност на F(18) се записва в масив. Стойността на F(19) се изчислява като се използва сумата от F(18) и F(17) и техните стойности вече са записани в масив. Изчислената стойност на F(19) се съхранява в масив. Стойността на F(20) може да бъде изчислена чрез добавяне на стойностите на F(19) и F(18), а стойностите на F(19) и F(18) се съхраняват в масив. Крайната изчислена стойност на F(20) се съхранява в масив.

Как работи подходът на динамичното програмиране?

Следват стъпките, които динамичното програмиране следва:

• Той разбива сложния проблем на по-прости подпроблеми.
• Той намира оптималното решение на тези подпроблеми.
• Съхранява резултатите от подпроблеми (мемоизация). Процесът на съхраняване на резултатите от подпроблемите е известен като запаметяване.
• Той ги използва повторно, така че същият подпроблем да се изчислява повече от веднъж.
• Накрая изчислете резултата от сложната задача.

Горните пет стъпки са основните стъпки за динамично програмиране. Динамичното програмиране е приложимо, което има свойства като:

как да конвертирате низ в char

Тези проблеми, които имат припокриващи се подпроблеми и оптимални подструктури. Тук оптималната подструктура означава, че решението на оптимизационните проблеми може да бъде получено чрез просто комбиниране на оптималното решение на всички подпроблеми.

В случай на динамично програмиране пространствената сложност ще се увеличи, тъй като съхраняваме междинните резултати, но времевата сложност ще бъде намалена.

Подходи на динамичното програмиране

Има два подхода към динамичното програмиране:

• Подход отгоре надолу
• Подход отдолу нагоре

Подход отгоре надолу

Подходът отгоре надолу следва техниката на запаметяване, докато подходът отдолу нагоре следва метода на таблично представяне. Тук запомнянето е равно на сумата от рекурсия и кеширане. Рекурсията означава извикване на самата функция, докато кеширането означава съхраняване на междинните резултати.

Предимства

• Много е лесно за разбиране и прилагане.
• Решава подпроблемите само когато е необходимо.
• Лесно е да се отстраняват грешки.

Недостатъци

cout

Той използва техниката на рекурсия, която заема повече памет в стека на повикванията. Понякога, когато рекурсията е твърде дълбока, ще възникне условието за препълване на стека.

Той заема повече памет, което влошава цялостната производителност.

Нека разберем динамичното програмиране чрез пример.

 int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of &apos;n&apos; increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td>  </tr><tr><td>Bottom-Up</td>  </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let&apos;s understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let&apos;s understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>