Дървото на изразите е дърво, използвано за представяне на различните изрази. Дървовидната структура от данни се използва за представяне на изразните изрази. В това дърво вътрешният възел винаги обозначава операторите.
- Листовите възли винаги обозначават операндите.
- Операциите винаги се извършват върху тези операнди.
- Операторът, присъстващ в дълбочината на дървото, винаги е с най-висок приоритет.
- Операторът, който не е много на дълбочина в дървото, винаги е с най-нисък приоритет в сравнение с операторите, разположени на дълбочина.
- Операндът винаги ще присъства в дълбочина на дървото; следователно се счита за най-висок приоритет сред всички оператори.
- Накратко, можем да го обобщим, тъй като стойността, присъстваща в дълбочина на дървото, е с най-висок приоритет в сравнение с другите оператори, присъстващи в горната част на дървото.
- Основната употреба на тези изразни дървета е, че се използва оценявам, анализирам и променям различните изрази.
- Използва се и за откриване на асоциативността на всеки оператор в израза.
- Например операторът + е ляв асоциативен, а / е десен асоциативен.
- Дилемата на тази асоциативност е изчистена с помощта на изразните дървета.
- Тези изразни дървета се формират чрез използване на безконтекстна граматика.
- Свързахме правило в безконтекстни граматики пред всяка граматична продукция.
- Тези правила са известни също като семантични правила и с помощта на тези семантични правила можем лесно да конструираме изразните дървета.
- Това е една от основните части на дизайна на компилатора и принадлежи към фазата на семантичния анализ.
- В този семантичен анализ ще използваме преводите, насочени към синтаксиса, и под формата на изход ще създадем анотираното дърво за анализ.
- Анотираното дърво за разбор не е нищо друго освен простото разбор, свързано с атрибута тип и всяко производствено правило.
- Основната цел на използването на изразните дървета е да се правят сложни изрази и могат лесно да бъдат оценени с помощта на тези изразни дървета.
- Той е неизменен и след като сме създали изразно дърво, не можем да го променяме или модифицираме допълнително.
- За да направите повече модификации, е необходимо да конструирате изцяло новото дърво на израза.
- Използва се и за решаване на оценката на постфикс, префикс и инфикс израз.
Изразните дървета играят много важна роля в представянето на езиково ниво код под формата на данни, които се съхраняват главно в дървовидна структура. Използва се и в представянето на паметта на ламбда изразяване. Използвайки дървовидната структура на данните, можем да изразим ламбда израза по-прозрачно и ясно. Първо се създава, за да преобразува кодовия сегмент в сегмента с данни, така че изразът да може лесно да бъде оценен.
Дървото на израза е двоично дърво, в което всеки външен или листов възел съответства на операнда и всеки вътрешен или родителски възел съответства на операторите, така че например дървото на израза за 7 + ((1+8)*3) би било:
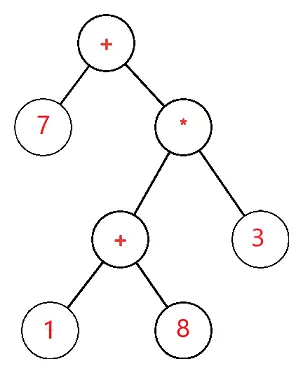
Нека S е изразното дърво
Ако S не е нула, тогава
Ако S.value е операнд, тогава
Върнете S.value
x = решаване (S.left)
y = решаване (S.right)
Върнете изчисление (x, y, S.value)
Тук, в горния пример, изразното дърво използва контекстно-свободна граматика.
Имаме някои продукции, свързани с някои производствени правила в тази граматика, известни главно като семантични правила . Можем да дефинираме генерирането на резултат от съответните производствени правила, използвайки тези семантични правила. Тук сме използвали стойностния параметър, който ще изчисли резултата и ще го върне към началния символ на граматиката. S.left ще изчисли лявото дете на възела и по подобен начин дясното дете на възела може да бъде изчислено с помощта на параметъра S.right.
Използване на дърво на израза
- Основната цел на използването на изразните дървета е да се правят сложни изрази и могат лесно да бъдат оценени с помощта на тези изразни дървета.
- Използва се и за откриване на асоциативността на всеки оператор в израза.
- Използва се и за решаване на оценката на постфикс, префикс и инфикс израз.
Реализация на дърво на израза
За да реализираме дървото на израза и да напишем неговата програма, ще трябва да използваме стекова структура от данни.
Тъй като знаем, че стекът се основава на принципа LIFO „последният влязъл, първи излязъл“, елементът от данни, който наскоро е бил избутан в стека, е бил изваден, когато е необходимо. За изпълнението му се използват основните две операции на стека, push и pop. Използвайки операцията push, ще избутаме елемента от данни в стека, а чрез операцията pop ще премахнем елемента от данни от стека.
Основни функции на стека в имплементацията на изразното дърво:
Първо, ще направим сканиране на дадения израз по начин отляво надясно, след което един по един ще проверим идентифицирания знак,
- Ако сканиран знак е операнд, ние ще приложим операцията за избутване и ще го поставим в стека.
- Ако сканиран знак е оператор, ние ще приложим операцията pop към него, за да премахнем двете стойности от стека, за да ги направим дъщерен, и след това ще върнем текущия родителски възел в стека.
Имплементация на Expression tree в езика за програмиране C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Резултатът от горната програма е:
X + Y * Z / W
Имплементация на Expression tree в езика за програмиране C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Резултатът от горната програма е:
X + Y * Z / W
Внедряване на Expression tree в езика за програмиране Java
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 