Дадени са три координати (x y), които са средата на страните на триъгълника. Задачата е да се намерят координатите на триъгълника.
Примери:
сортиране на купчина
Input : midx1 = 5 midy1 = 3 midx2 = 4 midy2 = 4 midx3 = 5 midy3 = 5 Output : x1 = 4 y1 = 2 x2 = 4 y2 = 6 x3 = 6 y3 = 4
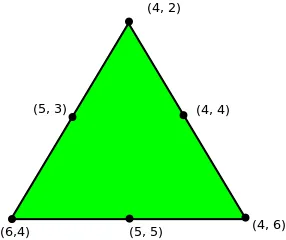
Solution can be verified by the figure.
Нека решим отделно за X-координати и Y-координати. За X координата на върховете нека те бъдат x1х2х3. Тогава X-координатата на средните точки ще бъде (x1+ x2)/2 (x2+ x3)/2 (x3+ x1)/2. Забележете, че сумата от тези 3 израза е равна на сумата от X-координати. Сега имаме сбор от 3 променливи и 3 израза за сумата на всяка двойка от тях, за да намерим стойностите на координатите чрез решаване на уравнения.
По подобен начин решаваме за Y-координати.
По-долу е изпълнението на този подход:
нормални формиC++
// C++ program to find coordinate of the // triangle given midpoint of each side #include
import java.util.Vector; // Java program to find coordinate of the // triangle given midpoint of each side class GFG { //static final int N = 3; // Return after solving the equations and // finding the vertices coordinate. static Vector<Integer> solve(int v[]) { Vector<Integer> res = new Vector<Integer>(); // Finding sum of all three coordinate. int all3 = v[0] + v[1] + v[2]; // Solving the equation. res.add(all3 - v[1] * 2); res.add(all3 - v[2] * 2); res.add(all3 - v[0] * 2); return res; } // Finds vertices of a triangles from given // middle vertices. static void findVertex(int xmid[] int ymid[]) { // Find X coordinates of vertices. Vector<Integer> V1 = solve(xmid); // Find Y coordinates of vertices. Vector<Integer> V2 = solve(ymid); // Output the solution. for (int i = 0; i < 3; i++) { System.out.println(V1.get(i) + ' ' + V2.get(i)); } } // Driver code public static void main(String[] args) { int xmid[] = {5 4 5}; int ymid[] = {3 4 5}; findVertex(xmid ymid); } } // This code is contributed by // PrinciRaj1992
# Python3 program to find coordinate of the # triangle given midpoint of each side N = 3 # Return after solving the equations and # finding the vertices coordinate. def solve(v): res = [] # Finding sum of all three coordinate. all3 = v[0] + v[1] + v[2] # Solving the equation. res.append(all3 - v[1] * 2) res.append(all3 - v[2] * 2) res.append(all3 - v[0] * 2) return res # Finds vertices of a triangles from given # middle vertices. def findVertex(xmid ymid): # Find X coordinates of vertices. V1 = solve(xmid) # Find Y coordinates of vertices. V2 = solve(ymid) # Output the solution. for i in range(0 3): print(V1[i] end=' ') print(V2[i]) # Driver code if __name__=='__main__': xmid = [5 4 5] ymid = [3 4 5] findVertex(xmid ymid) # This code is contributed by # Sanjit_Prasad
// C# program to find coordinate of the // triangle given midpoint of each side using System; using System.Collections; class GFG { //static final int N = 3; // Return after solving the equations and // finding the vertices coordinate. static ArrayList solve(int []v) { ArrayList res = new ArrayList(); // Finding sum of all three coordinate. int all3 = v[0] + v[1] + v[2]; // Solving the equation. res.Add(all3 - v[1] * 2); res.Add(all3 - v[2] * 2); res.Add(all3 - v[0] * 2); return res; } // Finds vertices of a triangles from given // middle vertices. static void findVertex(int []xmid int []ymid) { // Find X coordinates of vertices. ArrayList V1 = solve(xmid); // Find Y coordinates of vertices. ArrayList V2 = solve(ymid); // Output the solution. for (int i = 0; i < 3; i++) { Console.WriteLine(V1[i] + ' ' + V2[i]); } } // Driver code public static void Main() { int []xmid = {5 4 5}; int []ymid = {3 4 5}; findVertex(xmid ymid); } } // This code is contributed by mits
// PHP program to find coordinate of the // triangle given midpoint of each side $N = 3; // Return after solving the equations and // finding the vertices coordinate. function solve($v) { $res = array(); // Finding sum of all three coordinate. $all3 = $v[0] + $v[1] + $v[2]; // Solving the equation. array_push($res $all3 - $v[1] * 2); array_push($res $all3 - $v[2] * 2); array_push($res $all3 - $v[0] * 2); return $res; } // Finds vertices of a triangles from // given middle vertices. function findVertex($xmid $ymid) { // Find X coordinates of vertices. $V1 = solve($xmid); // Find Y coordinates of vertices. $V2 = solve($ymid); // Output the solution. for ($i = 0; $i < 3; $i++) print($V1[$i] . ' ' . $V2[$i] . 'n'); } // Driver code $xmid = array(5 4 5); $ymid = array(3 4 5); findVertex($xmid $ymid) // This code is contributed by mits ?> <script> // JavaScript program to find coordinate of the // triangle given midpoint of each side // Return after solving the equations and // finding the vertices coordinate. function solve(v) { var res = []; // Finding sum of all three coordinate. var all3 = v[0] + v[1] + v[2]; // Solving the equation. res.push(all3 - v[1] * 2); res.push(all3 - v[2] * 2); res.push(all3 - v[0] * 2); return res; } // Finds vertices of a triangles from given // middle vertices. function findVertex(xmid ymid) { // Find X coordinates of vertices. var V1 = solve(xmid); // Find Y coordinates of vertices. var V2 = solve(ymid); // Output the solution. for (var i = 0; i < 3; i++) { document.write(V1[i] + ' ' + V2[i] + '
'); } } // Driver code var xmid = [5 4 5]; var ymid = [3 4 5]; findVertex(xmid ymid); </script>
Изход:
6 4 4 2 4 6
Времева сложност: О(1)
Помощно пространство : O(1), защото използва постоянно пространство
опа концепции в java
