Алчният метод е една от стратегиите като Разделяй и владей, използвани за решаване на проблемите. Този метод се използва за решаване на оптимизационни проблеми. Проблемът с оптимизацията е проблем, който изисква максимални или минимални резултати. Нека разберем чрез някои термини.
Методът Greedy е най-простият и ясен подход. Това не е алгоритъм, но е техника. Основната функция на този подход е, че решението се взема на базата на наличната към момента информация. Каквато и текуща информация да е налице, решението се взема без да се тревожи за ефекта от текущото решение в бъдеще.
как да отворите json файл
Тази техника основно се използва за определяне на осъществимото решение, което може или не може да бъде оптимално. Осъществимото решение е подмножество, което отговаря на дадените критерии. Оптималното решение е решението, което е най-доброто и най-благоприятното решение в подгрупата. В случай на осъществимо, ако повече от едно решение удовлетворява дадените критерии, тогава тези решения ще се считат за осъществими, докато оптималното решение е най-доброто решение сред всички решения.
Характеристики на метода Greedy
Следните са характеристиките на алчен метод:
- За да конструира решението по оптимален начин, този алгоритъм създава два набора, като единият съдържа всички избрани елементи, а другият съдържа отхвърлените елементи.
- Алчният алгоритъм прави добри локални избори с надеждата, че решението трябва да бъде или осъществимо, или оптимално.
Компоненти на алчния алгоритъм
Компонентите, които могат да се използват в greedy алгоритъма са:
колко градове има в нас
Приложения на алчния алгоритъм
- Използва се за намиране на най-краткия път.
- Използва се за намиране на минималното обхващащо дърво с помощта на алгоритъма на Prim или алгоритъма на Kruskal.
- Използва се в последователност на работа с краен срок.
- Този алгоритъм се използва и за решаване на проблема с частичната раница.
Псевдо код на Greedy Algorithm
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Горното е алчният алгоритъм. Първоначално решението се присвоява с нулева стойност. Предаваме масива и броя на елементите в алчния алгоритъм. Вътре в цикъла for избираме елемента един по един и проверяваме дали решението е осъществимо или не. Ако решението е осъществимо, тогава извършваме обединението.
Нека разберем чрез пример.
Да предположим, че има проблем 'P'. Искам да пътувам от А до Б, както е показано по-долу:
P: A → B
Проблемът е, че трябва да изминем това пътуване от А до Б. Има различни решения за преминаване от А до Б. Можем да отидем от А до Б с пеша, кола, велосипед, влак, самолет и т.н. Има ограничение в пътуването, че трябва да изминем това пътуване в рамките на 12 часа. Само ако пътувам с влак или самолет, мога да измина това разстояние в рамките на 12 часа. Има много решения на този проблем, но има само две решения, които удовлетворяват ограничението.
Ако кажем, че трябва да покрием пътуването с минимални разходи. Това означава, че трябва да изминем това разстояние възможно най-малко, така че този проблем е известен като проблем за минимизиране. Досега имаме две осъществими решения, т.е. едно с влак и друго по въздух. Тъй като пътуването с влак ще доведе до минимални разходи, това е оптимално решение. Оптималното решение е и осъществимото решение, но осигуряващо най-добрия резултат, така че това решение да е оптималното решение с минимални разходи. Ще има само едно оптимално решение.
Проблемът, който изисква минимален или максимален резултат, тогава този проблем е известен като оптимизационен проблем. Greedy методът е една от стратегиите, използвани за решаване на оптимизационни проблеми.
javascript коментар
Недостатъци на използването на Greedy алгоритъм
Алчният алгоритъм взема решения въз основа на наличната информация на всяка фаза, без да отчита по-широкия проблем. Така че може да има възможност алчното решение да не дава най-доброто решение за всеки проблем.
Той следва местния оптимален избор на всеки етап с намерение да намери глобалния оптимум. Нека разберем чрез пример.
java concat низ
Разгледайте графиката, която е дадена по-долу:
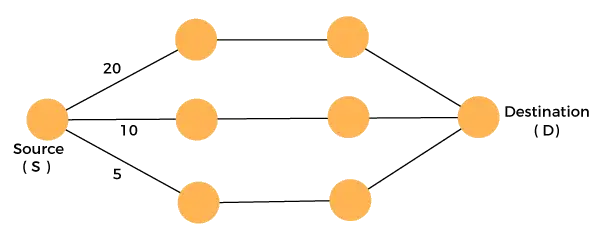
Трябва да пътуваме от източника до дестинацията с минимални разходи. Тъй като имаме три осъществими решения с пътеки на разходите като 10, 20 и 5. 5 е пътя на минималните разходи, така че това е оптималното решение. Това е локалният оптимум и по този начин намираме локалния оптимум на всеки етап, за да изчислим глобалното оптимално решение.
