• Алгоритъмът за изкачване на хълм е алгоритъм за локално търсене, който непрекъснато се движи в посока на нарастваща надморска височина/стойност, за да намери върха на планината или най-доброто решение на проблема. Прекратява се, когато достигне пикова стойност, при която никой съсед няма по-висока стойност.
• Алгоритъмът за изкачване на хълм е техника, която се използва за оптимизиране на математическите задачи. Един от широко обсъжданите примери за алгоритъм за изкачване на хълм е проблемът с търговския пътник, в който трябва да минимизираме разстоянието, изминато от продавача.
• Нарича се още алчно локално търсене, тъй като гледа само към доброто си непосредствено съседно състояние, а не отвъд това.
• Възелът на алгоритъма за изкачване на хълм има два компонента, които са състояние и стойност.
• Изкачването по хълм се използва най-вече, когато е налична добра евристика.
• В този алгоритъм не е необходимо да поддържаме и обработваме дървото или графиката за търсене, тъй като той запазва само едно текущо състояние.

Характеристики на катерене по хълм:

Следват някои основни характеристики на алгоритъма за катерене по хълм:

Генериране и тестване на вариант:Hill Climbing е вариантът на метода Generate and Test. Методът Генериране и тестване генерира обратна връзка, която помага да се реши в коя посока да се движи в пространството за търсене.Алчен подход:Търсенето на алгоритъм за катерене по хълм се движи в посока, която оптимизира разходите.Без връщане назад:Не връща назад в пространството за търсене, тъй като не помни предишните състояния.

Диаграма на пространството на състоянието за катерене по хълм:

Пейзажът на пространството на състоянията е графично представяне на алгоритъма за изкачване на хълм, който показва графика между различни състояния на алгоритъма и функцията на целта/цената.

На оста Y сме взели функцията, която може да бъде целева функция или функция на разходите, и пространството на състоянието на оста x. Ако функцията по Y-ос е цена, тогава целта на търсенето е да се намери глобалния минимум и локалния минимум. Ако функцията на Y-ос е Обективна функция, тогава целта на търсенето е да се намери глобалния максимум и локалния максимум.

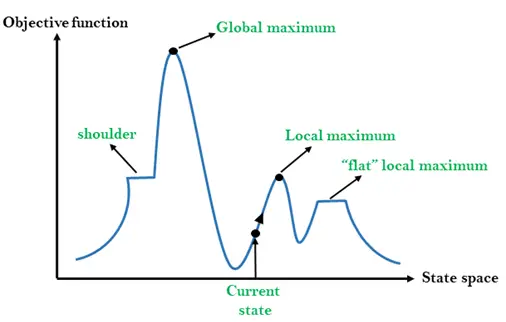
Различни региони в ландшафта на държавното пространство:

Местен максимум: Локалният максимум е състояние, което е по-добро от съседните му състояния, но има и друго състояние, което е по-високо от него.

Глобален максимум: Глобалният максимум е възможно най-доброто състояние на пространствения ландшафт на състоянието. Има най-висока стойност на обективна функция.

Сегашно състояние: Това е състояние в пейзажна диаграма, където в момента присъства агент.

Плосък локален максимум: Това е плоско пространство в пейзажа, където всички съседни държави на текущите държави имат еднаква стойност.

Рамо: Това е платовидна област, която има хълмист ръб.

Видове алгоритъм за катерене по хълм:

• Обикновено катерене по хълм:
• Изкачване на хълм с най-стръмно изкачване:
• Стохастично катерене по хълм:

1. Обикновено катерене по хълм:

Простото катерене по хълм е най-лесният начин за прилагане на алгоритъм за катерене по хълм. Той оценява само състоянието на съседния възел в даден момент и избира първия, който оптимизира текущата цена, и го задава като текущо състояние . Той само проверява, че това е едно наследствено състояние и ако намери по-добро от текущото състояние, тогава се премества, иначе ще бъде в същото състояние. Този алгоритъм има следните характеристики:

• Отнема по-малко време
• По-малко оптимално решение и решението не е гарантирано

Алгоритъм за просто катерене по хълм:

Етап 1:Оценете първоначалното състояние, ако е целево състояние, върнете успех и Стоп.Стъпка 2:Цикл Докато не бъде намерено решение или не остане нов оператор за прилагане.Стъпка 3:Изберете и приложете оператор към текущото състояние.Стъпка 4:Проверете новото състояние:
1. Ако е състояние на целта, тогава върнете успеха и излезте.
2. В противен случай, ако е по-добро от текущото състояние, тогава задайте ново състояние като текущо състояние.
3. В противен случай, ако не е по-добро от текущото състояние, тогава се върнете към стъпка 2.
Стъпка 5:Изход.

2. Изкачване на хълм с най-стръмно изкачване:

Алгоритъмът за най-стръмно изкачване е вариант на прост алгоритъм за изкачване на хълм. Този алгоритъм изследва всички съседни възли на текущото състояние и избира един съседен възел, който е най-близо до целевото състояние. Този алгоритъм отнема повече време, тъй като търси множество съседи

Алгоритъм за изкачване по хълм с най-стръмно изкачване:

Етап 1:Оценете първоначалното състояние, ако е целево състояние, върнете успех и спрете, в противен случай направете текущото състояние като първоначално състояние.Стъпка 2:Цикъл, докато се намери решение или текущото състояние не се промени.
1. Нека SUCC е такава държава, че всеки наследник на сегашната държава ще бъде по-добър от нея.
2. За всеки оператор, който се прилага към текущото състояние:
   1. Приложете новия оператор и генерирайте ново състояние.
   2. Оценете новото състояние.
   3. Ако е целево състояние, върнете го и излезте, в противен случай го сравнете със SUCC.
   4. Ако е по-добро от SUCC, тогава задайте ново състояние като SUCC.
   5. Ако SUCC е по-добър от текущото състояние, тогава задайте текущото състояние на SUCC.
Стъпка 5:Изход.

3. Стохастично изкачване на хълм:

Стохастичното изкачване на хълм не проверява за всички свои съседи, преди да се движи. По-скоро този алгоритъм за търсене избира един съседен възел на случаен принцип и решава дали да го избере като текущо състояние или да изследва друго състояние.

Проблеми в алгоритъма за катерене по хълм:

1. Местен максимум: Локален максимум е пиково състояние в пейзажа, което е по-добро от всяко от съседните му състояния, но има и друго състояние, което е по-високо от локалния максимум.

Решение: Техниката за обратно проследяване може да бъде решение на локалния максимум в ландшафта на пространството на състоянието. Създайте списък с обещаващия път, така че алгоритъмът да може да проследи назад в пространството за търсене и да проучи и други пътища.

2. Плато: Платото е плоската област на пространството за търсене, в която всички съседни състояния на текущото състояние съдържат една и съща стойност, тъй като този алгоритъм не намира най-добрата посока за движение. Търсене по хълм може да се загуби в района на платото.

Решение: Решението за платото е да се правят големи или много малки стъпки, докато се търси, за да се реши проблемът. Произволно изберете състояние, което е далеч от текущото състояние, така че е възможно алгоритъмът да намери област без плато.

3. Хребети: Гребенът е специална форма на локалния максимум. Той има площ, която е по-висока от околните райони, но самият той има наклон и не може да бъде достигнат с едно движение.

Решение: С използването на двупосочно търсене или като се движим в различни посоки, можем да подобрим този проблем.

Симулирано закаляване:

Алгоритъм за изкачване на хълм, който никога не прави движение към по-ниска стойност, гарантирано е непълен, защото може да се забие на локален максимум. И ако алгоритъмът приложи произволно ходене, като премести наследник, тогава той може да завърши, но не е ефективен. Симулирано закаляване е алгоритъм, който дава едновременно ефективност и пълнота.

В механичен смисъл Отгряване е процес на втвърдяване на метал или стъкло до висока температура, след което се охлажда постепенно, така че това позволява на метала да достигне нискоенергийно кристално състояние. Същият процес се използва при симулирано отгряване, при което алгоритъмът избира случаен ход, вместо да избира най-добрия ход. Ако произволният ход подобрява състоянието, тогава той следва същия път. В противен случай алгоритъмът следва пътя, който има вероятност по-малка от 1 или се движи надолу и избира друг път.