Линейната регресия и логистичната регресия са двата известни алгоритми за машинно обучение, които попадат в техниката на контролирано обучение. Тъй като и двата алгоритъма са контролирани по природа, следователно тези алгоритми използват етикетиран набор от данни, за да направят прогнозите. Но основната разлика между тях е как се използват. Линейната регресия се използва за решаване на регресионни проблеми, докато логистичната регресия се използва за решаване на проблеми с класификацията. Описанието на двата алгоритъма е дадено по-долу заедно с таблица на разликите.
Линейна регресия:
- Линейната регресия е един от най-простите алгоритъм за машинно обучение, който попада в техниката за контролирано обучение и се използва за решаване на проблеми с регресия.
- Използва се за прогнозиране на непрекъснатата зависима променлива с помощта на независими променливи.
- Целта на линейната регресия е да се намери най-подходящата линия, която може точно да предвиди изхода за непрекъснатата зависима променлива.
- Ако за прогнозиране се използва една независима променлива, тогава тя се нарича проста линейна регресия, а ако има повече от две независими променливи, тогава такава регресия се нарича множествена линейна регресия.
- Като намира най-подходящата линия, алгоритъмът установява връзката между зависима променлива и независима променлива. И връзката трябва да има линеен характер.
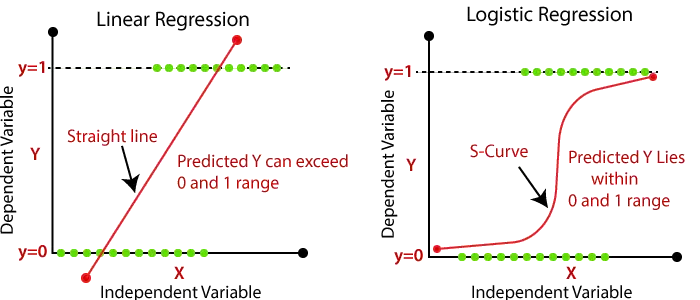
- Резултатът за линейната регресия трябва да бъде само непрекъснатите стойности като цена, възраст, заплата и т.н. Връзката между зависимата променлива и независимата променлива може да бъде показана на изображението по-долу:

В горното изображение зависимата променлива е на оста Y (заплата), а независимата променлива е на оста x (опит). Регресионната линия може да се запише като:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Къде0и а1са коефициентите, а ε е членът на грешката.
Логистична регресия:
- Логистичната регресия е един от най-популярните алгоритъм за машинно обучение, който попада в техниките за контролирано обучение.
- Може да се използва за класификация, както и за проблеми с регресия, но се използва главно за проблеми с класификация.
- Логистичната регресия се използва за прогнозиране на категоричната зависима променлива с помощта на независими променливи.
- Резултатът от проблема с логистичната регресия може да бъде само между 0 и 1.
- Логистичната регресия може да се използва, когато се изискват вероятностите между два класа. Като например дали ще вали днес или не, 0 или 1, вярно или невярно и т.н.
- Логистичната регресия се основава на концепцията за оценка на максималната вероятност. Според тази оценка, наблюдаваните данни трябва да са най-вероятни.
- В логистичната регресия ние предаваме претеглената сума на входовете през функция за активиране, която може да картографира стойности между 0 и 1. Такава функция за активиране е известна като сигмоидна функция и получената крива се нарича сигмоидна крива или S-крива. Разгледайте изображението по-долу:

- Уравнението за логистична регресия е:

Разлика между линейна регресия и логистична регресия:
| Линейна регресия | Логистична регресия |
|---|---|
| Линейната регресия се използва за прогнозиране на непрекъснатата зависима променлива с помощта на даден набор от независими променливи. | Логистичната регресия се използва за прогнозиране на категоричната зависима променлива, като се използва даден набор от независими променливи. |
| Линейната регресия се използва за решаване на регресионен проблем. | Логистичната регресия се използва за решаване на проблеми с класификацията. |
| При линейната регресия прогнозираме стойността на непрекъснатите променливи. | В логистичната регресия ние прогнозираме стойностите на категоричните променливи. |
| При линейната регресия намираме най-подходящата линия, чрез която можем лесно да предвидим изхода. | В логистичната регресия намираме S-кривата, по която можем да класифицираме пробите. |
| Методът на най-малкия квадрат се използва за оценка на точността. | За оценка на точността се използва методът за оценка на максималната вероятност. |
| Резултатът за линейна регресия трябва да бъде непрекъсната стойност, като цена, възраст и т.н. | Резултатът от логистичната регресия трябва да бъде категорична стойност като 0 или 1, Да или Не и т.н. |
| При линейната регресия се изисква връзката между зависимата променлива и независимата променлива да е линейна. | При логистичната регресия не се изисква да има линейна връзка между зависимата и независимата променлива. |
| При линейната регресия може да има колинеарност между независимите променливи. | При логистичната регресия не трябва да има колинеарност между независимата променлива. |
