• Pushdown automata е начин за внедряване на CFG по същия начин, по който проектираме DFA за обикновена граматика. DFA може да запомни ограничено количество информация, но PDA може да запомни безкрайно количество информация.
• Pushdown automata е просто NFA, допълнен с „външна стекова памет“. Добавянето на стека се използва за осигуряване на възможност за управление на паметта 'последен влязъл, първи излязъл' на Pushdown автомати. Pushdown автоматите могат да съхраняват неограничено количество информация в стека. Той има достъп до ограничено количество информация в стека. PDA може да избута елемент в горната част на стека и да изскочи елемент от върха на стека. За да прочетете елемент в стека, горните елементи трябва да бъдат извадени и да бъдат загубени.
• PDA е по-мощен от FA. Всеки език, който може да бъде приемлив от FA, може да бъде приемлив и от PDA. PDA също приема клас език, който дори не може да бъде приет от FA. Така PDA е много по-добър от FA.

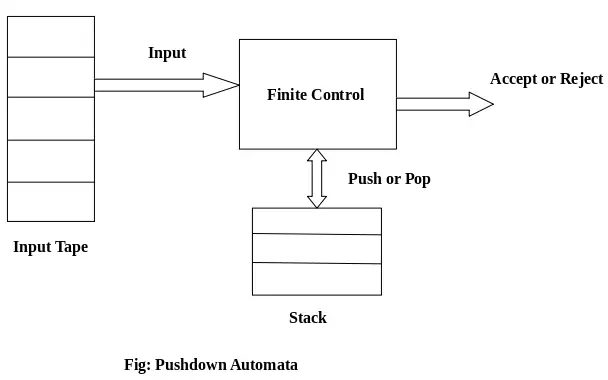
PDA компоненти:

Входна лента: Входната лента е разделена на много клетки или символи. Главата за въвеждане е само за четене и може да се движи само отляво надясно, един символ наведнъж.

Краен контрол: Крайният контрол има някакъв указател, който посочва текущия символ, който трябва да бъде прочетен.

Стек: Стекът е структура, в която можем да избутваме и премахваме елементите само от единия край. Има безкраен размер. В PDA стекът се използва за временно съхраняване на елементите.

Официална дефиниция на PDA:

PDA може да се определи като колекция от 7 компонента:

Q: крайното множество от състояния

∑: входния набор

° С: символ на стека, който може да бъде избутан и изваден от стека

q0: първоначалното състояние

java номер към низ

С: начален символ, който е в Γ.

Е: набор от крайни състояния

д: функция за картографиране, която се използва за преминаване от текущо състояние към следващо състояние.

Моментално описание (ID)

ID е неофициална нотация за това как PDA изчислява входен низ и взема решение дали низът е приет или отхвърлен.

Моментното описание е тройка (q, w, α), където:

р описва текущото състояние.

в описва оставащия вход.

базова лента срещу широколентова връзка

а описва съдържанието на стека, горе вляво.

Обозначение на турникета:

Знакът ⊢ описва обозначението на турникета и представлява едно движение.

⊢* знакът описва последователност от ходове.

Например,

(p, b, T) ⊢ (q, w, α)

В горния пример, докато се извършва преход от състояние p към q, входният символ 'b' се консумира и горната част на стека 'T' е представена от нов низ α.

Пример 1:

Проектирайте PDA за приемане на език a^нb²ⁿ.

Решение: На този език n на брой а трябва да бъде последвано от 2n на брой b. Следователно ще приложим много проста логика, а именно, ако прочетем едно „а“, ще избутаме две а в стека. Веднага след като прочетем 'b', тогава за всяко отделно 'b' само едно 'a' трябва да бъде извадено от стека.

parseint java

Идентификаторът може да бъде конструиран, както следва:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

Сега, когато прочетем b, ще променим състоянието от q0 на q1 и ще започнем да показваме съответното 'a'. следователно

 δ(q0, b, a) = (q1, ε) 

Така този процес на изскачане на 'b' ще се повтори, освен ако не бъдат прочетени всички символи. Обърнете внимание, че действието на изскачане се извършва само в състояние q1.

 δ(q1, b, a) = (q1, ε) 

След прочитане на всички b, всички съответстващи a трябва да бъдат извадени. Следователно, когато четем ε като входен символ, тогава не трябва да има нищо в стека. Следователно движението ще бъде:

 δ(q1, ε, Z) = (q2, ε) 

Където

монитор с катодна тръба

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

Можем да обобщим идентификатора като:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

Сега ще симулираме този PDA за входния низ 'aaabbbbbb'.

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

Пример 2:

Проектирайте PDA за приемане на език 0^н1^м0^н.

Решение: В този PDA n на брой нули са последвани от произволен брой 1, последвани от n на брой 0. Следователно логиката за проектиране на такъв PDA ще бъде следната:

Избутайте всички нули в стека, когато срещнете първите нули. Тогава, ако прочетем 1, просто не правим нищо. След това прочетете 0 и при всяко прочитане на 0 извадете една 0 от стека.

Например:

Този сценарий може да бъде написан във формата за идентификация като:

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

Сега ще симулираме този PDA за входния низ '0011100'.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT