В тази статия ще обсъдим обхождането на дървото в структурата на данните. Терминът „преминаване на дърво“ означава преминаване или посещение на всеки възел на дърво. Има един единствен начин за преминаване през линейната структура на данни като свързан списък, опашка и стек. Като има предвид, че има множество начини за преминаване през дърво, които са изброени, както следва -
- Обхождане на предварителна поръчка
- Обхождане по ред
- Преминаване на пощенски поръчки
И така, в тази статия ще обсъдим изброените по-горе техники за преминаване през дърво. Сега нека започнем да обсъждаме начините за обхождане на дърво.
Обхождане на предварителна поръчка
Тази техника следва политиката „root left right“. Това означава, че първият основен възел се посещава, след което лявото поддърво се обхожда рекурсивно и накрая, дясното поддърво се обхожда рекурсивно. Тъй като основният възел се преминава преди (или преди) лявото и дясното поддърво, това се нарича обхождане с предварителна поръчка.
Така че при обхождане с предварителна поръчка всеки възел се посещава преди двете му поддървета.
Приложенията на обхождане на предварителна поръчка включват -
- Използва се за създаване на копие на дървото.
- Може също да се използва за получаване на префиксния израз на изразно дърво.
Алгоритъм
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Пример
Сега, нека видим примера на техниката за обхождане на предварителна поръчка.
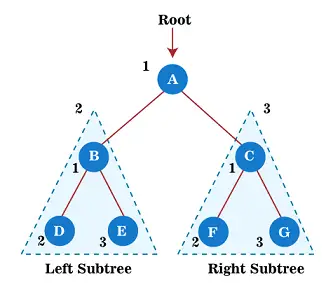
Сега започнете да прилагате обхождането на предварителната поръчка върху горното дърво. Първо преминаваме през коренния възел А; след това преминете към лявото поддърво Б , които също ще бъдат обходени в предварителна поръчка.
И така, за ляво поддърво B, първо, коренният възел Б преминава се самата; след това, лявото му поддърво д се преминава. Тъй като възел д няма деца, преместете се в дясно поддърво И . Тъй като възел E също няма деца, обхождането на лявото поддърво на коренния възел A е завършено.
вътрешна работа на hashmap
Сега се придвижете към дясното поддърво на коренния възел A, което е C. И така, за дясното поддърво C, първо коренния възел ° С прекоси себе си; след това, лявото му поддърво Е се преминава. Тъй като възел Е няма деца, преместете се в дясното поддърво Ж . Тъй като възел G също няма деца, обхождането на дясното поддърво на коренния възел A е завършено.
Следователно всички възли на дървото се пресичат. И така, изходът от обхождането на предварителната поръчка на горното дърво е -
A → B → D → E → C → F → G
За да научите повече за обхождането на предварителната поръчка в структурата на данните, можете да следвате връзката Обхождане на предварителна поръчка .
Преминаване на пощенски поръчки
Тази техника следва политиката „ляв-десен корен“. Това означава, че се преминава през първото ляво поддърво на основния възел, след това рекурсивно преминава през дясното поддърво и накрая се преминава през основния възел. Тъй като основният възел се преминава след (или след) лявото и дясното поддърво, това се нарича преминаване след поръчка.
И така, при обхождане след поръчка, всеки възел се посещава след двете си поддървета.
Приложенията на прехода след поръчка включват -
java конвертира цяло число в низ
- Използва се за изтриване на дървото.
- Може също да се използва за получаване на постфиксния израз на изразно дърво.
Алгоритъм
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Пример
Сега нека видим примера на техниката за преминаване след поръчка.

Сега започнете да прилагате прехода след поръчка върху горното дърво. Първо преминаваме през лявото поддърво B, което ще бъде обходено в последващ ред. След това ще преминем през дясното поддърво ° С по поръчка. И накрая, основният възел на горното дърво, т.е. А , се преминава.
И така, за лявото поддърво B, първо, неговото ляво поддърво д се преминава. Тъй като възел д няма деца, преминете през дясното поддърво И . Тъй като възел E също няма деца, преминете към основния възел Б. След преминаване на възел Б, преминаването на лявото поддърво на коренния възел A е завършено.
Сега се придвижете към дясното поддърво на коренния възел A, което е C. И така, за дясното поддърво C, първо лявото му поддърво Е се преминава. Тъй като възел Е няма деца, преминете през дясното поддърво Ж . Тъй като възел G също няма деца, следователно, накрая, основният възел на дясното поддърво, т.е. ° С, се преминава. Обхождането на дясното поддърво на коренния възел A е завършено.
Най-накрая преминете през коренния възел на дадено дърво, т.е. А . След преминаване през коренния възел, последващото обхождане на даденото дърво е завършено.
Следователно всички възли на дървото се пресичат. И така, резултатът от обхождането след поръчка на горното дърво е -
D → E → B → F → G → C → A
За да научите повече за преминаването след поръчка в структурата на данните, можете да следвате връзката Преминаване на пощенски поръчки .
Обхождане по ред
Тази техника следва политиката „left root right“. Това означава, че първото ляво поддърво е посетено след преминаването на този основен възел и накрая е обходено дясното поддърво. Тъй като основният възел се преминава между лявото и дясното поддърво, той се нарича преминаване по ред.
размер латексов шрифт
И така, при обхождането по ред, всеки възел се посещава между своите поддървета.
Приложенията на Inorder traversal включват -
- Използва се за получаване на BST възлите в нарастващ ред.
- Може също да се използва за получаване на префиксния израз на изразно дърво.
Алгоритъм
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Пример
Сега нека видим примера на техниката за преминаване по ред.

Сега започнете да прилагате обхождането по ред върху горното дърво. Първо преминаваме през лявото поддърво Б които ще бъдат преминати в ред. След това ще преминем през основния възел А . И накрая дясното поддърво ° С се преминава в ред.
И така, за лявото поддърво Б , първо, лявото му поддърво д се преминава. Тъй като възел д няма деца, така че след като го обходите, възел Б ще бъде обходено и накрая дясно поддърво на възел B, т.е И , се преминава. Възел E също няма деца; следователно преминаването на лявото поддърво на коренния възел А е завършено.
След това преминете през коренния възел на дадено дърво, т.е. А .
Най-накрая се придвижете към дясното поддърво на коренния възел A, което е C. И така, за дясното поддърво C; първо, лявото му поддърво Е се преминава. Тъй като възел Е няма деца, възел ° С ще бъде обходено и накрая дясно поддърво на възел C, т.е. Ж , се преминава. Възел G също няма деца; следователно преминаването на дясното поддърво на коренния възел A е завършено.
кога излезе win 7
Тъй като всички възли на дървото са обходени, обхождането по ред на даденото дърво е завършено. Резултатът от обхождането по ред на горното дърво е -
D → B → E → A → F → C → G
За да научите повече за преминаването по ред в структурата на данните, можете да следвате връзката Обхождане по ред .
Сложност на техниките за обхождане на дърво
Времевата сложност на техниките за обхождане на дърво, обсъдени по-горе, е На) , където 'н' е размерът на двоичното дърво.
Докато пространствената сложност на техниките за обхождане на дървета, обсъдени по-горе, е О(1) ако не вземем предвид размера на стека за извиквания на функции. В противен случай космическата сложност на тези техники е O(h) , където 'ч' е височината на дървото.
Внедряване на обхождане на дърво
Сега нека видим изпълнението на гореобсъдените техники с помощта на различни езици за програмиране.
програма: Напишете програма за прилагане на техники за обхождане на дърво в C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Изход

програма: Напишете програма за прилагане на техники за обхождане на дърво в C#.
string.valueof java
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Изход

програма: Напишете програма за прилагане на техники за обхождане на дърво в C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Изход
След изпълнението на горния код, изходът ще бъде -

Заключение
В тази статия обсъдихме различните видове техники за обхождане на дървото: обхождане преди поръчка, обхождане по ред и обхождане след поръчка. Виждали сме тези техники заедно с алгоритъм, пример, сложност и имплементация в C, C++, C# и java.
И така, това е всичко за статията. Надяваме се, че ще ви бъде полезно и информативно.
