Преди разбирането Б дърво и B+ дърво разлики, трябва да знаем B дървото и B+ дървото поотделно.
Какво е дървото B?
Б дърво е самобалансиращо се дърво и е m-way дърво, където m определя реда на дървото. Btree е обобщение на Двоично дърво за търсене в който възел може да има повече от един ключ и повече от две деца в зависимост от стойността на м . В дървото B данните са посочени в сортиран ред с по-ниски стойности в лявото поддърво и по-високи стойности в дясното поддърво.
урок по микроуслуги
Свойства на B дърво
Следните са свойствата на B дървото:
- В B дървото всички листови възли трябва да са на едно и също ниво, докато в случай на двоично дърво листовите възли могат да бъдат на различни нива.
Нека разберем това свойство чрез пример.
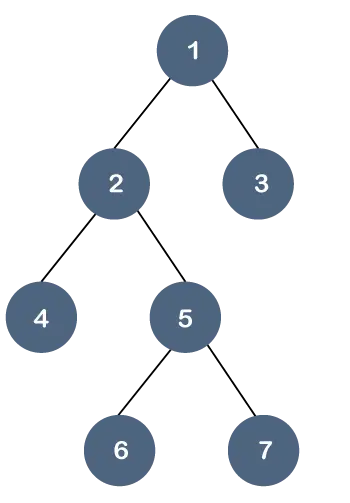
В горното дърво всички листови възли не са на едно и също ниво, но имат най-много две деца. Следователно можем да кажем, че горното дърво е a двоично дърво но не и B дърво.
- Ако Btree има ред от m, тогава всеки възел може да има максимум м В случай на минимални деца, листовите възли имат нула деца, коренният възел има две деца, а вътрешните възли имат таван от m/2.
- Всеки възел може да има максимум (m-1) ключове. Например, ако стойността на m е 5, тогава максималната стойност на ключовете е 4.
- Основният възел има минимум един ключ, докато всички останали възли с изключение на основния възел имат (таван от m/2 минус - 1) минимум ключове.
- Ако извършим вмъкване в B дървото, тогава възелът винаги се вмъква в листовия възел.
Да предположим, че искаме да създадем B дърво от ред 3, като вмъкнем стойности от 1 до 10.
Етап 1: Първо създаваме възел с 1 стойност, както е показано по-долу:

Стъпка 2: Следващият елемент е 2, който идва след 1, както е показано по-долу:

Стъпка 3: Следващият елемент е 3 и се вмъква след 2, както е показано по-долу:

Тъй като знаем, че всеки възел може да има 2 максимални ключа, така че ще разделим този възел през средния елемент. Средният елемент е 2, така че се премества към своя родител. Възел 2 няма родител, така че ще стане основен възел, както е показано по-долу:

Стъпка 4: Следващият елемент е 4. Тъй като 4 е по-голямо от 2 и 3, той ще бъде добавен след 3, както е показано по-долу:

Стъпка 5: Следващият елемент е 5. Тъй като 5 е по-голямо от 2, 3 и 4, то ще бъде добавено след 4, както е показано по-долу:

Тъй като знаем, че всеки възел може да има 2 максимални ключа, така че ще разделим този възел през средния елемент. Средният елемент е 4, така че се премества към своя родител. Родителят е възел 2; следователно 4 ще се добави след 2, както е показано по-долу:

Стъпка 6: Следващият елемент е 6. Тъй като 6 е по-голямо от 2, 4 и 5, така че 6 ще дойде след 5, както е показано по-долу:

Стъпка 7: Следващият елемент е 7. Тъй като 7 е по-голямо от 2, 4, 5 и 6, така че 7 ще дойде след 6, както е показано по-долу:

Тъй като знаем, че всеки възел може да има 2 максимални ключа, така че ще разделим този възел през средния елемент. Средният елемент е 6, така че се премества към своя родител, както е показано по-долу:

Но 6 не може да се добави след 4, защото възелът може да има 2 максимални ключа, така че ще разделим този възел през средния елемент. Средният елемент е 4, така че се премества към своя родител. Тъй като възел 4 няма родител, възел 4 ще стане основен възел, както е показано по-долу:

Какво е B+ дърво?
The B+ дърво е известен също като усъвършенствано самобалансирано дърво, защото всеки път от корена на дървото до листа на дървото има еднаква дължина. Тук същата дължина означава, че всички листови възли се намират на едно и също ниво. Няма да се случи някои от листните възли да се появят на трето ниво, а някои от тях на второ ниво.
B+ дървовидният индекс се счита за многостепенен индекс, но B+ дървовидната структура не е подобна на последователните файлове на многостепенния индекс.
Защо се използва дървото B+?
B+ дърво се използва за съхраняване на записите много ефективно чрез съхраняване на записите по индексиран начин с помощта на B+ дървовидна индексирана структура. Благодарение на многостепенното индексиране, достъпът до данни става по-бърз и лесен.
B+ дървовидна възлова структура
Структурата на възлите на B+ дървото съдържа указатели и ключови стойности, показани на фигурата по-долу:

Както можем да забележим в горната структура на B+ дървовиден възел, че тя съдържа n-1 ключови стойности (k1към кn-1) и n указателя (стр1Горна частн).
Стойностите на ключовете за търсене, които са поставени във възела, се съхраняват в сортиран ред. По този начин, ако i
Ограничение за различни видове възли
Нека 'b' е редът на дървото B+.
Non-Leaf възел
Нека 'm' представлява броя на децата на възел, тогава връзката между реда на дървото и броя на децата може да бъде представена като:

Нека k представлява стойностите на ключа за търсене. Връзката между реда на дървото и ключа за търсене може да бъде представена като:
Тъй като знаем, че броят на указателите е равен на стойностите на ключа за търсене плюс 1, така че математически може да се запише като:
Брой указатели (или деца) = Брой клавиши за търсене + 1
Следователно максималният брой указатели ще бъде 'b', а минималният брой указатели ще бъде таванната функция на b/2.
Листен възел
hashset java
Листовият възел е възел, който се появява на последното ниво на B+ дървото и всеки листов възел използва само един указател, за да се свърже един с друг, за да осигури последователен достъп на листовото ниво.
В листовия възел максималният брой деца е:

Максималният брой ключове за търсене е:

Коренен възел
Максималният брой деца в случай на коренния възел е: b
Минималният брой деца е: 2
Специални случаи в B+ дърво
Случай 1: Ако коренният възел е единственият възел в дървото. В този случай коренният възел става листовият възел.
В този случай максималният брой деца е 1, т.е. самият коренов възел, докато минималният брой деца е b-1, което е същото като това на листовия възел.
Представяне на листен възел в B+ дърво

В горната фигура, '.' представлява указателя, докато 10, 20 и 30 са ключовите стойности. Указателят съдържа адреса, на който се съхранява стойността на ключа, както е показано на фигурата по-горе.
Пример за B+ дърво

В горната фигура възелът съдържа три ключови стойности, т.е. 9, 16 и 25. Указателят, който се появява преди 9, съдържа ключовите стойности, по-малки от 9, представени от kаз. Указателят, който се появява преди 16, съдържа ключовите стойности, по-големи или равни на 9, но по-малки от 16, представени от kj. Указателят, който се появява преди 25, съдържа ключовите стойности, по-големи или равни на 16, но по-малки от 25, представени от kн.
Разлики между B дърво и B+ дърво

Следните са разликите между B дърво и B+ дърво:
| Б дърво | B+ дърво |
|---|---|
| В B дървото всички ключове и записи се съхраняват както във вътрешни, така и в листови възли. | В дървото B+ ключовете са индексите, съхранявани във вътрешните възли, а записите се съхраняват в листовите възли. |
| В B дърво ключовете не могат да се съхраняват многократно, което означава, че няма дублиране на ключове или записи. | В дървото B+ може да има излишък при появата на ключовете. В този случай записите се съхраняват в листовите възли, докато ключовете се съхраняват във вътрешните възли, така че излишните ключове могат да присъстват във вътрешните възли. |
| В Btree листовите възли не са свързани един с друг. | В B+ дърво, листовите възли са свързани един с друг, за да осигурят последователен достъп. |
| В Btree търсенето не е много ефективно, защото записите се съхраняват или в листа, или във вътрешни възли. | В B+ дърво търсенето е много ефективно или по-бързо, защото всички записи се съхраняват в листовите възли. |
| Изтриването на вътрешни възли е много бавен и отнема много време процес, тъй като трябва да вземем предвид и детето на изтрития ключ. | Изтриването в B+ дърво е много бързо, защото всички записи се съхраняват в листовите възли, така че не трябва да вземаме предвид дъщерния елемент на възела. |
| В Btree последователният достъп не е възможен. | В дървото B+ всички листови възли са свързани помежду си чрез указател, така че е възможен последователен достъп. |
| В Btree се извършват по-голям брой операции за разделяне, поради което височината се увеличава в сравнение с ширината, | B+ дървото има повече ширина в сравнение с височина. |
| В Btree всеки възел има най-малко два клона и всеки възел съдържа някои записи, така че не е необходимо да преминаваме до листовите възли, за да получим данните. | В B+ дърво вътрешните възли съдържат само указатели, а листовите възли съдържат записи. Всички листови възли са на едно и също ниво, така че трябва да преминем до листовите възли, за да получим данните. |
| Коренният възел съдържа най-малко 2 до m деца, където m е редът на дървото. | Коренният възел съдържа най-малко 2 до m деца, където m е редът на дървото. |
