В тази статия ще обсъдим двоичното дърво за търсене. Тази статия ще бъде много полезна и информативна за студентите с техническо образование, тъй като е важна тема от техния курс.
Преди да преминем директно към дървото за двоично търсене, нека първо видим кратко описание на дървото.
Какво е дърво?
Дървото е вид структура от данни, която се използва за представяне на данните в йерархична форма. Може да се дефинира като колекция от обекти или обекти, наречени възли, които са свързани заедно, за да симулират йерархия. Дървото е нелинейна структура от данни, тъй като данните в дърво не се съхраняват линейно или последователно.
Сега нека започнем темата, дървото за двоично търсене.
char tostring java
Какво е двоично дърво за търсене?
Едно двоично дърво за търсене следва някакъв ред за подреждане на елементите. В двоично дърво за търсене стойността на левия възел трябва да е по-малка от родителския възел, а стойността на десния възел трябва да е по-голяма от родителския възел. Това правило се прилага рекурсивно към лявото и дясното поддървета на корена.
Нека разберем концепцията за двоично дърво за търсене с пример.
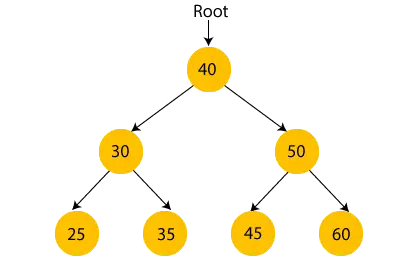
На фигурата по-горе можем да видим, че коренният възел е 40 и всички възли на лявото поддърво са по-малки от коренния възел, а всички възли на дясното поддърво са по-големи от коренния възел.
По подобен начин можем да видим лявото дете на коренния възел е по-голямо от лявото дете и по-малко от дясното дете. Така че, той също така отговаря на свойството на двоично дърво за търсене. Следователно можем да кажем, че дървото в горното изображение е двоично дърво за търсене.
Да предположим, че ако променим стойността на възел 35 на 55 в горното дърво, проверете дали дървото ще бъде двоично дърво за търсене или не.

В горното дърво стойността на коренния възел е 40, което е по-голямо от лявото му дете 30, но по-малко от дясното дете на 30, т.е. 55. Така че горното дърво не отговаря на свойството на двоично дърво за търсене. Следователно горното дърво не е двоично дърво за търсене.
Предимства на дървото за двоично търсене
- Търсенето на елемент в дървото за двоично търсене е лесно, тъй като винаги имаме подсказка кое поддърво съдържа желания елемент.
- В сравнение с масиви и свързани списъци, операциите по вмъкване и изтриване са по-бързи в BST.
Пример за създаване на двоично дърво за търсене
Сега нека видим създаването на двоично дърво за търсене, използвайки пример.
mvc за java
Да предположим, че елементите от данни са - 45, 15, 79, 90, 10, 55, 12, 20, 50
- Първо, трябва да вмъкнем Четири пет в дървото като корен на дървото.
- След това прочетете следващия елемент; ако е по-малък от основния възел, вмъкнете го като корен на лявото поддърво и преминете към следващия елемент.
- В противен случай, ако елементът е по-голям от коренния възел, тогава го вмъкнете като корен на дясното поддърво.
Сега нека видим процеса на създаване на двоично дърво за търсене с помощта на дадения елемент от данни. Процесът на създаване на BST е показан по-долу -
Стъпка 1 - Поставете 45.

Стъпка 2 - Поставете 15.
Тъй като 15 е по-малко от 45, вмъкнете го като основен възел на лявото поддърво.

Стъпка 3 - Поставете 79.
Тъй като 79 е по-голямо от 45, вмъкнете го като коренния възел на дясното поддърво.

Стъпка 4 - Поставете 90.
90 е по-голямо от 45 и 79, така че ще бъде вмъкнато като дясно поддърво на 79.

Стъпка 5 - Поставете 10.
10 е по-малко от 45 и 15, така че ще бъде вмъкнато като ляво поддърво на 15.
колко клавиша имат клавиатурите

Стъпка 6 - Поставете 55.
55 е по-голямо от 45 и по-малко от 79, така че ще бъде вмъкнато като ляво поддърво на 79.

Стъпка 7 - Поставете 12.
12 е по-малко от 45 и 15, но по-голямо от 10, така че ще бъде вмъкнато като дясно поддърво на 10.

Стъпка 8 - Поставете 20.
20 е по-малко от 45, но по-голямо от 15, така че ще бъде вмъкнато като дясно поддърво на 15.

Стъпка 9 - Поставете 50.
50 е по-голямо от 45, но по-малко от 79 и 55. Така че ще бъде вмъкнато като ляво поддърво на 55.

Сега създаването на двоично дърво за търсене е завършено. След това нека преминем към операциите, които могат да бъдат извършени в двоично дърво за търсене.
Можем да извършваме операции за вмъкване, изтриване и търсене в двоичното дърво за търсене.
Нека разберем как се извършва търсене в дърво за двоично търсене.
Търсене в двоично дърво за търсене
Търсене означава намиране или локализиране на конкретен елемент или възел в структура от данни. В двоично дърво за търсене търсенето на възел е лесно, защото елементите в BST се съхраняват в определен ред. Стъпките за търсене на възел в дървото на двоично търсене са изброени както следва -
- Първо сравнете елемента, който ще търсите, с коренния елемент на дървото.
- Ако root съвпада с целевия елемент, връща местоположението на възела.
- Ако не съвпадне, проверете дали елементът е по-малък от коренния елемент, ако е по-малък от коренния елемент, след това преминете към лявото поддърво.
- Ако е по-голям от коренния елемент, тогава се преместете в дясното поддърво.
- Повторете горната процедура рекурсивно, докато се намери съвпадението.
- Ако елементът не е намерен или не присъства в дървото, връща NULL.
Сега нека разберем търсенето в двоично дърво, използвайки пример. Взимаме двоичното дърво за търсене, образувано по-горе. Да предположим, че трябва да намерим възел 20 от дървото по-долу.
Етап 1:

Стъпка 2:

Стъпка 3:

Сега нека видим алгоритъма за търсене на елемент в дървото за двоично търсене.
Алгоритъм за търсене на елемент в двоично дърво за търсене
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> Изход
arraylist.sort
След изпълнението на горния код, изходът ще бъде -

И така, това е всичко за статията. Надяваме се, че статията ще ви бъде полезна и информативна.
