В този раздел ще обсъдим метода за конвертиране на NFA в неговия еквивалент DFA. В NFA, когато се даде конкретен вход на текущото състояние, машината преминава в множество състояния. Може да има нула, един или повече от един ход върху даден входен символ. От друга страна, в DFA, когато се даде конкретен вход към текущото състояние, машината преминава само в едно състояние. DFA има само един ход върху даден входен символ.
Нека M = (Q, ∑, δ, q0, F) е NFA, който приема езика L(M). Трябва да има еквивалентен DFA, означен с M' = (Q', ∑', q0', δ', F'), така че L(M) = L(M').
Стъпки за конвертиране на NFA в DFA:
Етап 1: Първоначално Q' = ϕ
Стъпка 2: Добавете q0 от NFA към Q'. След това намерете преходите от това начално състояние.
Стъпка 3: В Q' намерете възможния набор от състояния за всеки входен символ. Ако този набор от състояния не е в Q', тогава го добавете към Q'.
обвиване на css текст
Стъпка 4: В DFA крайното състояние ще бъдат всички състояния, които съдържат F (крайни състояния на NFA)
Пример 1:
Преобразувайте дадения NFA в DFA.
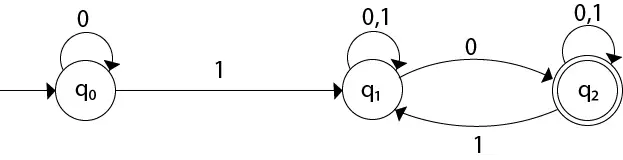
Решение: За дадената диаграма на прехода първо ще построим таблицата на прехода.
| състояние | 0 | 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | {q1, q2} | q1 |
| *q2 | q2 | {q1, q2} |
Сега ще получим δ' преход за състояние q0.
δ'([q0], 0) = [q0] δ'([q0], 1) = [q1]
Преходът δ' за състояние q1 се получава като:
какво прави компютъра бърз
δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1]
Преходът δ' за състояние q2 се получава като:
δ'([q2], 0) = [q2] δ'([q2], 1) = [q1, q2]
Сега ще получим δ' преход върху [q1, q2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] Състоянието [q1, q2] също е крайното състояние, защото съдържа крайно състояние q2. Преходната таблица за конструирания DFA ще бъде:
| състояние | 0 | 1 |
|---|---|---|
| →[q0] | [q0] | [q1] |
| [q1] | [q1, q2] | [q1] |
| *[q2] | [q2] | [q1, q2] |
| *[q1, q2] | [q1, q2] | [q1, q2] |
Диаграмата на прехода ще бъде:

Състоянието q2 може да бъде елиминирано, защото q2 е недостижимо състояние.
задайте java
Пример 2:
Преобразувайте дадения NFA в DFA.

Решение: За дадената диаграма на прехода първо ще построим таблицата на прехода.
| състояние | 0 | 1 |
|---|---|---|
| →q0 | {q0, q1} | {q1} |
| *q1 | ϕ | {q0, q1} |
Сега ще получим δ' преход за състояние q0.
δ'([q0], 0) = {q0, q1} = [q0, q1] (new state generated) δ'([q0], 1) = {q1} = [q1] Преходът δ' за състояние q1 се получава като:
δ'([q1], 0) = ϕ δ'([q1], 1) = [q0, q1]
Сега ще получим δ' преход на [q0, q1].
δ'([q0, q1], 0) = δ(q0, 0) ∪ δ(q1, 0) = {q0, q1} ∪ ϕ = {q0, q1} = [q0, q1] По същия начин,
δ'([q0, q1], 1) = δ(q0, 1) ∪ δ(q1, 1) = {q1} ∪ {q0, q1} = {q0, q1} = [q0, q1] Тъй като в дадения NFA q1 е крайно състояние, тогава в DFA където и да съществува q1 това състояние става крайно състояние. Следователно в DFA крайните състояния са [q1] и [q0, q1]. Следователно набор от крайни състояния F = {[q1], [q0, q1]}.
шаблон за проектиране на фабричен метод
Преходната таблица за конструирания DFA ще бъде:
| състояние | 0 | 1 |
|---|---|---|
| →[q0] | [q0, q1] | [q1] |
| *[q1] | ϕ | [q0, q1] |
| *[q0, q1] | [q0, q1] | [q0, q1] |
Диаграмата на прехода ще бъде:

Дори можем да променим името на щатите на DFA.
Да предположим
A = [q0] B = [q1] C = [q0, q1]
С тези нови имена DFA ще бъде както следва:

