Многобройните начини, по които данните могат да бъдат подредени, записани и обработвани в компютърна програма, се наричат структури от данни в Java. Тези структури предлагат методичен метод за ефективно боравене и управление на данни, като позволяват полезни операции като вмъкване, изтриване, извличане и обхождане.
Статията ще изследва всичко, свързано със структурите от данни в Java, и помага на начинаещите да разбират лесно и ефективно.
- Какво е Java?
- Какво представляват структурите от данни в Java?
- Типове структури от данни в Java
- Предимства на структурите от данни в Java
- Класификация на структурите от данни
- Структури на данни в Java Често задавани въпроси
Какво е Java?
Java е популярен обектно-ориентиран език за програмиране, известен със своята огромна стандартна библиотека и свобода на платформата. Той предлага солидна архитектура за създаване на програми, работещи без повторно компилиране в различни платформи. Добре известната библиотека за Java има избор от системи за записи, които я правят жизнеспособна за ефективна работа с множество типове данни.
Какво представляват структурите от данни в Java?
Начинът, по който данните се организират и съхраняват в паметта на компютърната програма, зависи в голяма степен от структурите на записи на Java. Добре известната библиотека на Java включва значителен тип вградени статистически структури. Някои от системите за записи, които позволяват на програмистите кратки и прости начини за запазване и подреждане на данни, включват свързани списъци, стекове, опашки и масиви. Разработчиците могат бързо да извършват операции като вмъкване, изтриване, търсене и сортиране, защото предоставят набор от механизми за получаване на достъп до, промяна и управление на данни. Java програмистите могат да намалят използването на памет и значително да повишат общата ефективност на своите програми, като използват тези структури от данни.
Типове структури от данни в Java
Списъкът със структури от данни в Java е посочен по-долу
- Масиви
- ArrayList
- LinkedList
- Стек
- Опашка
- HashMap
- HashSet
- TreeSet
- TreeMap
- Графика
- Дърво
Диаграмата по-долу ясно обяснява много ясно типовете структури от данни в Java.
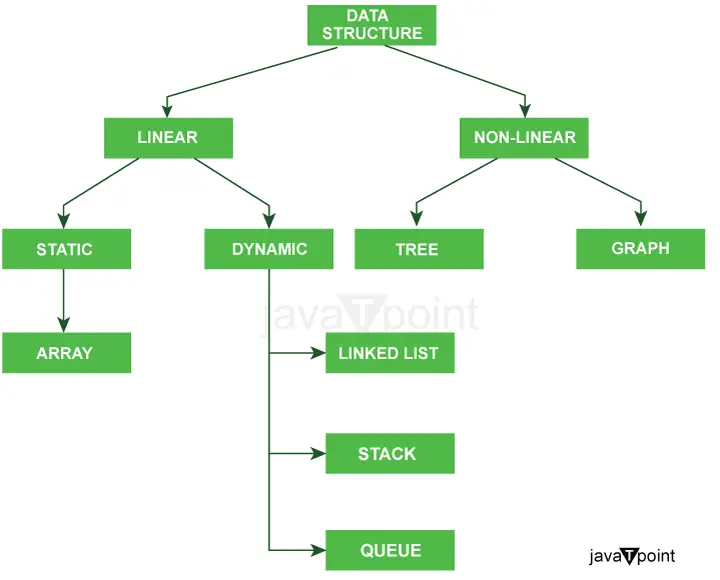
Допълнителна класификация на типовете структури от данни:
Има два типа структури от данни: -
- Примитивни структури от данни
- Непримитивни структури от данни
1) Примитивни структури от данни: Известни също като примитивни типове данни, това са основни вградени типове данни в Java. Те включват:
2) Непримитивни структури от данни: Структурите на непримитивните записи са по-сложни и се състоят от примитивни видове информация. Освен това те могат да бъдат категоризирани в два вида:

Предимства на структурите от данни в Java
1) Масиви:
Масивът е основна и често използвана структура от данни в контекста на структурите от данни на Java. Той предлага метод за съхраняване на колекция с фиксиран размер от компоненти от идентичен тип. Тъй като осигуряват бърз и лесен достъп до елементи в зависимост от техния индекс, масивите са ключов инструмент за управление и организиране на данни.
Предимства:
Недостатъци:
Функции:
Изпълнение:
Име на файл: ArrayExample.java
import java.util.*; public class ArrayExample { public static void main(String[] args) { int[] numbers={10,20,30,40,50}; // Initialize an array of integers System.out.println('Element at index 0:'+numbers[0]); System.out.println('Element at index 2:'+numbers[2]); System.out.println('Element at index 4:'+numbers[4]); int sum=0; for (int i=0;i<numbers.length;i++) { sum+="numbers[i];" } system.out.println('sum of array elements:'+sum); numbers[2]="35;" update an element in the system.out.println('updated at index 2:'+numbers[2]); system.out.println('elements array:'); for (int number:numbers) system.out.println(number); < pre> <p> <strong>Output:</strong> </p> <pre> Element at index 0:10 Element at index 2:30 Element at index 4:50 Sum of array elements:150 Updated element at index 2:35 Elements in the array: 10 20 35 40 50 </pre> <h3>2) ArrayList:</h3> <p>ArrayList in Java is a dynamic data structure that allows for the storage and manipulation of elements. It is part of the Java Collections Framework and is implemented using an array internally.</p> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Dynamic Size:</td> Unlike arrays, ArrayLists can dynamically grow or shrink in size as elements are added or removed. It eliminates the need for manual resizing and allows for handling varying amounts of data conveniently. </tr><tr><td>Easy Element Manipulation:</td> ArrayLists offer methods to add, remove, and modify elements at any position within the list. Its flexibility simplifies common operations such as insertion, deletion, and updating, making element manipulation more efficient. </tr><tr><td>Random Access:</td> ArrayLists support random Access to elements using their index, enabling quick retrieval and modification of elements at specific positions within the list. It facilitates efficient element access and enhances overall performance. </tr><tr><td>Compatibility with Java Collection Framework:</td> ArrayLists implement the List interface, making them compatible with other Collection classes in the Java Collections Framework. Its compatibility allows for seamless integration with various algorithms and operations provided by the framework. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>Higher Memory Overhead:</td> ArrayLists require additional memory to maintain their internal structure, resulting in higher memory overhead compared to arrays. It can be a concern when dealing with large collections of elements. </tr><tr><td>Slower Insertion and Deletion:</td> Inserting or deleting elements in the middle of an ArrayList requires shifting elements, which can be time-consuming for large lists. In scenarios where frequent insertion or deletion operations are expected, other data structures like LinkedList may offer better performance. </tr><tr><td>Limited Performance for Search:</td> Searching for an element in an unsorted ArrayList requires iterating over the elements until a match is found. It is a linear search approach that results in slower search performance compared to data structures optimized for searching, such as HashSet or TreeMap. </tr><tr><td>No Primitive Type Support:</td> ArrayLists can only store objects and do not directly support primitive data types like int or char. To store primitive types, wrapper classes like Integer or Character need to be used, leading to potential autoboxing and unboxing overhead. </tr></ol> <p> <strong>Functions:</strong> </p> <ol class="points"> <tr><td>Creating an ArrayList:</td> Declare and initialize an ArrayList using the ArrayList class and specify the element type within the angle brackets. </tr><tr><td>Adding Elements:</td> Use the add method to append elements at the end of the ArrayList. </tr><tr><td>Accessing Elements:</td> Use the get technique to retrieve the price of detail at a selected index. </tr><tr><td>Modifying Elements:</td> Update the cost of detail at a specific index for the usage of the set approach. </tr><tr><td>Finding Size:</td> Use the dimensions method to get the cutting-edge quantity of factors in the ArrayList. </tr><tr><td>Removing Elements:</td> Use the remove approach to delete a detail at a specific index or via providing the object reference. </tr><tr><td>Iterating through the ArrayList:</td> Use loops to iterate over each element in the ArrayList and perform operations on them. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> ArrayListExample.java</p> <pre> import java.util.*; public class ArrayListExample { public static void main(String[] args) { // Create an ArrayList to store integers ArrayList numbers=new ArrayList(List.of(10,20,30,40,50)); //Access and print elements from the ArrayList System.out.println('Element at index 0:'+numbers.get(0)); System.out.println('Element at index 2:'+numbers.get(2)); System.out.println('Element at index 4:'+numbers.get(4)); // Calculate and print the sum of all elements in the ArrayList int sum=numbers.stream().mapToInt(Integer::intValue).sum(); System.out.println('Sum of ArrayList elements:'+sum); // Update an element in the ArrayList numbers.set(2,35); System.out.println('Updated element at index 2:'+numbers.get(2)); // Iterate through the ArrayList using a for-each loop and print the elements System.out.println('Elements in the ArrayList:'); for (int number:numbers) { System.out.println(number); } } } </pre> <p> <strong>Output:</strong> </p> <pre> Element at index 0:10 Element at index 2:30 Element at index 4:50 Sum of ArrayList elements:150 Updated element at index 2:35 Elements in the ArrayList: 10 20 35 40 50 </pre> <h3>3) Linked List:</h3> <p>A linked list is a linear data structure in which elements are stored in separate objects called nodes. A reference link to the following node in the sequence is included in each node's data element. The list's final node links to null, indicating that the list has ended.</p> <p>Unlike arrays, linked lists do not require contiguous memory allocation. Each node in a linked list can be allocated independently, allowing for dynamic memory allocation and efficient insertion and deletion operations.</p> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Dynamic Size:</td> LinkedList can grow or shrink dynamically, making it suitable for varying or unknown data sizes. </tr><tr><td>Efficient Insertion and Deletion:</td> Inserting or deleting elements within a LinkedList is efficient, as it does not require shifting elements. </tr><tr><td>No Contiguous Memory Requirement:</td> LinkedList does not need contiguous memory allocation, making it flexible and suitable for unpredictable memory situations. </tr><tr><td>Easy Modification:</td> LinkedList allows easy modification of elements by changing reference pointers, enabling efficient manipulation. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>Slower Random Access:</td> LinkedList has slower random Access as it requires traversing the list to access elements by index. </tr><tr><td>Increased Memory Overhead:</td> LinkedList requires additional memory for references and nodes, increasing memory overhead compared to arrays. </tr><tr><td>Inefficient Search:</td> LinkedList has slower search operations, requiring sequential iteration to find specific elements. </tr></ol> <p> <strong>Functions:</strong> </p> <ol class="points"> <tr><td>Creating a LinkedList:</td> Declare and initialize a LinkedList using the LinkedList class. </tr><tr><td>Adding Elements:</td> Use the add method to append elements at the end of the LinkedList. </tr><tr><td>Accessing Elements:</td> Use the get method to retrieve the value of an element at a specific index. </tr><tr><td>Modifying Elements:</td> Update the value of an element at a particular index using the set method. </tr><tr><td>Removing Elements:</td> Use the remove method to delete an element at a specific index or by providing the object reference. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> LinkedList1.java</p> <pre> import java.util.*; public class LinkedList1 { public static void main(String[] args) { // Create a LinkedList to store integers LinkedList linkedList1 = new LinkedList(); // Add elements to the LinkedList linkedList1.add(10); linkedList1.add(20); linkedList1.add(30); linkedList1.add(40); linkedList1.add(50); // Print the LinkedList System.out.println('LinkedList:'+linkedList1); // Remove an element from the LinkedList linkedList1.removeFirst(); System.out.println('LinkedList after removing first element:'+linkedList1); // Check if an element exists in the LinkedList boolean containsElement=linkedList1.contains(30); System.out.println('LinkedList contains element 30?'+containsElement); // Get the first and last elements of the LinkedList int firstElement=linkedList1.getFirst(); int lastElement=linkedList1.getLast(); System.out.println('First element:'+firstElement); System.out.println('Last element:'+lastElement); // Clear the LinkedList linkedList1.clear(); System.out.println('LinkedList after clearing:'+linkedList1); } } </pre> <p> <strong>Output:</strong> </p> <pre> LinkedList:[10, 20, 30, 40, 50] LinkedList after removing first element:[20, 30, 40, 50] LinkedList contains element 30?true First element:20 Last element:50 LinkedList after clearing:[] </pre> <h3>4) Stack:</h3> <p>The Last-In-First-Out (LIFO) principle dictates that the element that was most recently inserted is also the element that is removed first. A stack is a linear data structure that follows this rule. It employs the commands 'push' and 'pop' to add elements to the stack and, accordingly, remove the top element from the stack. The 'peek' technique additionally enables Access to the top element without removing it.</p> <p> <strong>Features of a stack:</strong> </p> <ol class="points"> <tr><td>LIFO behavior:</td> The last element pushed onto the stack is the first one to be popped out, making it suitable for applications where the order of insertion and removal is important. </tr><tr><td>Limited Access:</td> Stacks typically provide restricted Access to elements. You can only access the topmost element, and to reach other elements, you need to pop the elements above them. </tr><tr><td>Dynamic size:</td> Stacks can be implemented using arrays or linked lists, allowing for a dynamic size. They can grow or shrink as needed during runtime. </tr></ol> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Simplicity:</td> Stacks are easy to understand and implement. </tr><tr><td>Efficiency:</td> Insertion and deletion operations have a time complexity of O(1). </tr><tr><td>Function call management:</td> Stacks efficiently manage function calls and variable storage. </tr><tr><td>Undo/Redo functionality:</td> Stacks enable undo and redo operations in applications. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>Limited Access:</td> Access to elements is restricted to the top of the stack. </tr><tr><td>Size restrictions:</td> Stacks may have size limitations depending on the implementation. </tr><tr><td>Not suitable for all scenarios:</td> Stacks are specific to LIFO behavior and may not be appropriate in other cases. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> StackExample.java</p> <pre> import java.util.Stack; public class StackExample { public static void main(String[] args) { // Create a stack Stack stack=new Stack(); // Push elements onto the stack stack.push(10); stack.push(20); stack.push(30); // Print the top element of the stack System.out.println('Top element:'+stack.peek()); // Pop elements from the stack int poppedElement=stack.pop(); System.out.println('Popped element:'+poppedElement); // Check if the stack is empty System.out.println('Is stack empty?'+stack.isEmpty()); // Get the size of the stack System.out.println('Stack size:'+stack.size()); // Iterate over the stack System.out.println('Stack elements:'); for (Integer element:stack) { System.out.println(element); } } } </pre> <p> <strong>Output:</strong> </p> <pre> Top element:30 Popped element:30 Is stack empty?false Stack size:2 Stack elements: 10 20 </pre> <h3>5) Queue:</h3> <p>A queue is a linear data structure in Java that follows the First-In-First-Out (FIFO) principle. It represents a collection of elements where elements are inserted at the rear and removed from the front.</p> <p> <strong>Features:</strong> </p> <ol class="points"> <tr><td>Enqueue:</td> Adding an element to the rear of the queue. </tr><tr><td>Dequeue:</td> Removing an element from the front of the queue. </tr><tr><td>Peek:</td> Retrieve the element at the front of the queue without removing it. </tr><tr><td>Size:</td> Determining the number of elements in the queue. </tr><tr><td>Empty Check:</td> Checking if the queue is empty. </tr></ol> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>FIFO Behavior:</td> Elements are processed in the order of their insertion, ensuring the preservation of the original sequence. </tr><tr><td>Efficient Insertion and Removal:</td> Adding and removing elements from a queue is fast and has a constant time complexity of O(1). </tr><tr><td>Synchronization:</td> Java provides synchronized queue implementations, making them safe for concurrent programming. </tr><tr><td>Standardized Interface:</td> The Queue interface in Java offers a common set of methods, allowing easy interchangeability between different queue implementations. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>No Random Access:</td> Queues do not support direct Access to elements in the middle. Accessing specific positions requires dequeuing preceding elements. </tr><tr><td>Limited Size:</td> Some queue implementations have a fixed size or capacity, leading to overflow or exceptions when exceeding the maximum size. </tr><tr><td>Inefficient Search:</td> Searching for an element in a queue requires dequeuing until a match is found, resulting in a linear search with potentially high time complexity. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> QueueExample.java</p> <pre> import java.util.Stack; import java.util.LinkedList; import java.util.Queue; public class QueueExample { public static void main(String[] args) { // Create a Queue to store integers Queue queue=new LinkedList(); // Enqueue elements to the Queue queue.offer(10); queue.offer(20); queue.offer(30); queue.offer(40); queue.offer(50); //Access and print the front element of the Queue System.out.println('Front element:'+queue.peek()); // Dequeue elements from the Queue and print them while (!queue.isEmpty()) { int element=queue.poll(); System.out.println('Dequeued element:'+element); } } } </pre> <p> <strong>Output:</strong> </p> <pre> Front element:10 Dequeued element:10 Dequeued element:20 Dequeued element:30 Dequeued element:40 Dequeued element:50 </pre> <h3>6) HashMap:</h3> <p>A HashMap is a data structure in Java that provides a way to store and retrieve key-value pairs. It is part of the Java Collections Framework and is implemented based on the hash table data structure.</p> <p> <strong>Functions:</strong> </p> <ul> <tr><td>put(key, value):</td> Inserts the specified key-value pair into the HashMap. </tr><tr><td>get(key):</td> Retrieves the value associated with the specified key. </tr><tr><td>containsKey(key):</td> Checks if the HashMap contains the specified key. </tr><tr><td>containsValue(value):</td> Checks if the HashMap contains the specified value. </tr><tr><td>remove(key):</td> Removes the key-value pair associated with the specified key from the HashMap. </tr><tr><td>size():</td> Returns the number of key-value pairs in the HashMap. </tr><tr><td>isEmpty():</td> Checks if the HashMap is empty. </tr><tr><td>keySet():</td> Returns a Set containing all the keys in the HashMap. </tr><tr><td>values():</td> Returns a Collection containing all the values in the HashMap. </tr><tr><td>clear():</td> Removes all the key-value pairs from the HashMap. </tr></ul> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Efficient Retrieval:</td> HashMap provides fast retrieval of values based on keys with constant-time complexity O(1). </tr><tr><td>Flexible Key-Value Pairing:</td> HashMap allows any non-null object as a key, enabling custom-defined keys for storing and retrieving data. </tr><tr><td>Dynamic Size:</td> HashMap can dynamically grow or shrink in size to handle varying amounts of data. </tr><tr><td>Compatibility with Java Collections Framework:</td> HashMap implements the Map interface, allowing seamless integration with other Collection classes. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>Lack of Ordering:</td> HashMap does not preserve the order of elements. Use LinkedHashMap or TreeMap for specific ordering requirements. </tr><tr><td>Increased Memory Overhead:</td> HashMap requires additional memory for hash codes and internal structure compared to simpler data structures. </tr><tr><td>Slower Iteration:</td> Iterating over a HashMap can be slower compared to arrays or lists due to traversing the underlying hash table. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> HashMapExample.java</p> <pre> import java.util.HashMap; public class HashMapExample { public static void main(String[] args) { // Create a HashMap to store String keys and Integer values HashMap hashMap=new HashMap(); // Add key-value pairs to the HashMap hashMap.put('John',25); hashMap.put('Alice',30); hashMap.put('Bob',35); //Access and print values based on keys System.out.println('Age of John:'+hashMap.get('John')); System.out.println('Age of Alice:'+hashMap.get('Alice')); // Check if a key exists in the HashMap System.out.println('Is Bob present?'+hashMap.containsKey('Bob')); // Update the value associated with a key hashMap.put('Alice',32); // Remove a key-value pair from the HashMap hashMap.remove('John'); // Print all key-value pairs in the HashMap System.out.println('Key-Value pairs in the HashMap:'); for (String key : hashMap.keySet()) { System.out.println(key+':'+hashMap.get(key)); } // Check the size of the HashMap System.out.println('Size of the HashMap:'+hashMap.size()); } } </pre> <p> <strong>Output:</strong> </p> <pre> Age of John:25 Age of Alice:30 Is Bob present?true Key-Value pairs in the HashMap: Bob:35 Alice:32 Size of the HashMap:2 </pre> <h3>7) HashSet:</h3> <p>HashSet is a data structure in Java that implements the Set interface and stores elements in a hash table.</p> <p> <strong>Features:</strong> </p> <ol class="points"> <tr><td>Stores unique elements:</td> HashSet does not allow duplicate elements. Each element in the HashSet is unique. </tr><tr><td>Uses hash-based lookup:</td> HashSet uses the hash value of each element to determine its storage location, providing efficient element retrieval. </tr><tr><td>Unordered collection:</td> The elements in a HashSet are not stored in a specific order. The order of elements may change over time. </tr></ol> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Fast element lookup:</td> HashSet provides fast lookup operations, making it efficient to check if an element exists in the set. </tr><tr><td>No duplicate elements:</td> HashSet automatically handles duplicate elements and ensures that each element is unique. </tr><tr><td>Integration with Java Collections Framework:</td> HashSet implements the Set interface, making it compatible with other collection classes in the Java Collections Framework. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>No guaranteed order:</td> HashSet does not maintain the order of elements. If the order of elements is important, HashSet is not suitable. </tr><tr><td>No indexing:</td> HashSet does not provide direct indexing or positional Access to elements. To access elements, you need to iterate over the set. </tr><tr><td>Higher memory overhead:</td> HashSet requires additional memory to store hash values and maintain the hash table structure, resulting in higher memory usage compared to some other data structures. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> HashSetExample.java</p> <pre> import java.util.HashSet; public class HashSetExample { public static void main(String[] args) { // Create a HashSet HashSet set=new HashSet(); // Add elements to the HashSet set.add('Apple'); set.add('Banana'); set.add('Orange'); set.add('Grapes'); set.add('Mango'); // Print the HashSet System.out.println('HashSet:'+set); // Check if an element exists System.out.println('Contains 'Apple':'+set.contains('Apple')); // Remove an element set.remove('Banana'); // Print the updated HashSet System.out.println('Updated HashSet:'+set); // Get the size of the HashSet System.out.println('Size of HashSet:'+set.size()); // Clear the HashSet set.clear(); // Check if the HashSet is empty System.out.println('Is HashSet empty?'+set.isEmpty()); } } </pre> <p> <strong>Output:</strong> </p> <pre> HashSet:[Apple, Grapes, Mango, Orange, Banana] Contains 'Apple':true Updated HashSet:[Apple, Grapes, Mango, Orange] Size of HashSet:4 Is HashSet empty?true </pre> <h3>8) TreeSet:</h3> <p>TreeSet is an implementation of the SortedSet interface in Java that uses a self-balancing binary search tree called a red-black tree to store elements in sorted order.</p> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Sorted Order:</td> TreeSet automatically maintains the elements in a sorted order based on their natural ordering or a custom comparator. It allows for efficient searching and retrieval of elements in ascending or descending order. </tr><tr><td>No Duplicate Elements:</td> TreeSet does not allow duplicate elements. It ensures that each element in the set is unique, which can be useful in scenarios where duplicate values should be avoided. </tr><tr><td>Efficient Operations:</td> TreeSet provides efficient operations like insertion, deletion, and searching. These operations have a time complexity of O(log n), where n is the number of elements in the set. </tr><tr><td>Navigable Set Operations:</td> TreeSet provides additional navigational methods, such as higher(), lower(), ceiling(), and floor(), which allow you to find elements that are greater than, less than, or equal to a given value. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>Overhead:</td> TreeSet requires additional memory to store the internal data structure, which can lead to higher memory overhead compared to other set implementations. </tr><tr><td>Slower Insertion and Removal:</td> Insertion and removal operations in TreeSet involve maintaining the sorted order of elements, which may require tree restructuring. It can make these operations slightly slower compared to HashSet or LinkedHashSet. </tr><tr><td>Limited Customization:</td> TreeSet is primarily designed for natural ordering or a single custom comparator. It may need more flexibility for multiple sorting criteria or complex sorting logic. </tr></ol> <p> <strong>Functions:</strong> </p> <ul> <tr><td>add(element):</td> Adds an element to the TreeSet while maintaining the sorted order. </tr><tr><td>remove(element):</td> Removes the specified element from the TreeSet. </tr><tr><td>contains(element):</td> Checks if the TreeSet contains the specified element. </tr><tr><td>size():</td> Returns the number of elements in the TreeSet. </tr><tr><td>first():</td> Returns the first (lowest) element in the TreeSet. </tr><tr><td>last():</td> Returns the last (highest) element in the TreeSet. </tr><tr><td>higher(element):</td> Returns the least element in the TreeSet that is strictly greater than the given element. </tr><tr><td>lower(element):</td> Returns the greatest element in the TreeSet that is strictly less than the given element. </tr></ul> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> TreeSetExample.java</p> <pre> import java.util.TreeSet; public class TreeSetExample { public static void main(String[] args) { // Create a TreeSet TreeSet numbers=new TreeSet(); // Add elements to the TreeSet numbers.add(5); numbers.add(2); numbers.add(8); numbers.add(1); numbers.add(4); // Print the TreeSet System.out.println('Elements in the TreeSet:'+numbers); // Check if an element exists System.out.println('Does TreeSet contain 4?'+numbers.contains(4)); // Remove an element numbers.remove(2); // Print the TreeSet after removal System.out.println('Elements in the TreeSet after removal:'+numbers); // Get the size of the TreeSet System.out.println('Size of the TreeSet:'+numbers.size()); // Get the first and last element System.out.println('First element:'+numbers.first()); System.out.println('Last element:'+numbers.last()); // Iterate over the TreeSet System.out.println('Iterating over the TreeSet:'); for (int number:numbers) { System.out.println(number); } } } </pre> <p> <strong>Output:</strong> </p> <pre> Elements in the TreeSet:[1, 2, 4, 5, 8] Does TreeSet contain 4? true Elements in the TreeSet after removal:[1, 4, 5, 8] Size of the TreeSet:4First element:1 Last element:8 Iterating over the TreeSet: 1 4 5 8 </pre> <h3>9) TreeMap:</h3> <p>TreeMap is a class in Java that implements the Map interface and provides a sorted key-value mapping based on the natural order of the keys or a custom comparator.</p> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Sorted Ordering:</td> TreeMap maintains the keys in sorted order, which allows for efficient searching, retrieval, and range-based operations. </tr><tr><td>Key-Value Mapping:</td> TreeMap stores key-value pairs, enabling efficient lookup and retrieval of values based on the associated keys. </tr><tr><td>Red-Black Tree Implementation:</td> TreeMap uses a balanced binary search tree (Red-Black Tree) internally, ensuring efficient performance even for large datasets. </tr><tr><td>Support for Custom Comparators:</td> TreeMap allows the use of custom comparators to define the sorting order of the keys, providing flexibility in sorting criteria. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>Memory Overhead:</td> TreeMap requires additional memory to store the internal tree structure and associated objects, resulting in higher memory usage compared to simpler data structures like HashMap. </tr><tr><td>Slower Insertion and Deletion:</td> Insertion and deletion operations in TreeMap have a time complexity of O(log n) due to the need for tree restructuring, making them slower compared to HashMap or LinkedHashMap. </tr><tr><td>Limited Performance for Unsorted Data:</td> TreeMap performs efficiently for sorted data, but its performance can degrade when dealing with unsorted data or frequent modifications, as it requires maintaining the sorted order. </tr></ol> <p> <strong>Functions:</strong> </p> <ul> <tr><td>put(key, value):</td> Inserts a key-value pair into the TreeMap. </tr><tr><td>get(key):</td> Retrieves the value associated with the specified key. </tr><tr><td>containsKey(key):</td> Checks if the TreeMap contains a specific key. </tr><tr><td>remove(key):</td> Removes the key-value pair associated with the specified key. </tr><tr><td>size():</td> Returns the number of key-value pairs in the TreeMap. </tr><tr><td>keySet():</td> Returns a set of all keys in the TreeMap. </tr><tr><td>values():</td> Returns a collection of all values in the TreeMap. </tr><tr><td>entrySet():</td> Returns a set of key-value pairs in the TreeMap. </tr></ul> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> TreeMapExample.java</p> <pre> import java.util.TreeMap; public class TreeMapExample { public static void main(String[] args) { // Create a TreeMap TreeMap scores=new TreeMap(); // Insert key-value pairs into the TreeMap scores.put('Alice',90); scores.put('Bob',80); scores.put('Charlie',95); scores.put('David',87); scores.put('Eve',92); //Access and print values from the TreeMap System.out.println('Score of Alice:'+scores.get('Alice')); System.out.println('Score of Charlie:'+scores.get('Charlie')); System.out.println('Score of David:'+scores.get('David')); // Update a value in the TreeMap scores.put('Bob',85); // Remove a key-value pair from the TreeMap scores.remove('Eve'); // Iterate through the TreeMap using a for-each loop System.out.println('Scores in the TreeMap:'); for (String name:scores.keySet()) { int score=scores.get(name); System.out.println(name+':'+score); } } } </pre> <p> <strong>Output:</strong> </p> <pre> Score of Alice:90 Score of Charlie:95 Score of David:87 Scores in the TreeMap: Alice:90 Bob:85 Charlie:95 David:87 </pre> <h3>10) Graph:</h3> <p>Graphs are data structure that represents a collection of interconnected nodes or vertices. They are composed of vertices and edges, where vertices represent entities and edges represent the relationships between those entities.</p> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Versatility:</td> Graphs can represent a wide range of real-world scenarios, making them suitable for various applications such as social networks, transportation systems, and computer networks. </tr><tr><td>Relationship Representation:</td> Graphs provide a natural way to represent relationships and connections between entities, allowing for efficient analysis and traversal of these relationships. </tr><tr><td>Efficient Search and Traversal:</td> Graph algorithms like breadth-first search (BFS) and depth-first search (DFS) enable efficient traversal and searching of the graph's vertices and edges. </tr><tr><td>Modeling Complex Relationships:</td> Graphs can model complex relationships, including hierarchical structures, cyclic dependencies, and multiple connections between entities. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>Space Complexity:</td> Graphs can consume a significant amount of memory, especially large-scale graphs with many vertices and edges. </tr><tr><td>The complexity of Operations:</td> Certain graph operations, such as finding the shortest path or detecting cycles, can have high time complexity, particularly in dense graphs. </tr><tr><td>Difficulty in Maintenance:</td> Modifying or updating a graph can be complex, as changes in the graph's structure may impact its connectivity and existing algorithms. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> GraphExample.java</p> <pre> import java.util.*; public class GraphExample { private int V; // Number of vertices private List<list> adjacencyList; // Adjacency list representation public GraphExample(int V) { this.V=V; adjacencyList=new ArrayList(V); // Initialize the adjacency list for (int i=0;i<v;i++) { adjacencylist.add(new arraylist()); } function to add an edge between two vertices public void addedge(int source,int destination) adjacencylist.get(source).add(destination); adjacencylist.get(destination).add(source); perform breadth-first search traversal of the graph bfs(int startvertex) boolean[] visited="new" boolean[v]; queue linkedlist(); visited[startvertex]="true;" queue.add(startvertex); while (!queue.isempty()) int currentvertex="queue.poll();" system.out.print(currentvertex+' '); list neighbors="adjacencyList.get(currentVertex);" for (int neighbor:neighbors) if (!visited[neighbor]) visited[neighbor]="true;" queue.add(neighbor); system.out.println(); depth-first dfs(int dfsutil(startvertex,visited); private dfsutil(int vertex,boolean[] visited) visited[vertex]="true;" system.out.print(vertex+' dfsutil(neighbor,visited); static main(string[] args) v="5;" number graphexample graphexample(v); edges graph.addedge(0,1); graph.addedge(0,2); graph.addedge(1,3); graph.addedge(2,3); graph.addedge(2,4); system.out.print('bfs traversal: graph.bfs(0); system.out.print('dfs graph.dfs(0); < pre> <p> <strong>Output:</strong> </p> <pre> BFS traversal: 0 1 2 3 4 DFS traversal: 0 1 3 2 4 </pre> <h3>11) Tree:</h3> <p>A tree is a widely used data structure in computer science that represents a hierarchical structure. It consists of nodes connected by edges, where each node can have zero or more child nodes.</p> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Hierarchical Structure:</td> Trees provide a natural way to represent hierarchical relationships, such as file systems, organization charts, or HTML/XML documents. </tr><tr><td>Efficient Search:</td> Binary search trees enable efficient searching with a time complexity of O(log n), making them suitable for storing and retrieving sorted data. </tr><tr><td>Fast Insertion and Deletion:</td> Tree data structures offer efficient insertion and deletion operations, especially when balanced, such as AVL trees or Red-Black trees. </tr><tr><td>Ordered Iteration:</td> In-order traversal of a binary search tree gives elements in a sorted order, which is helpful for tasks like printing elements in sorted order or finding the next/previous element. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>High Memory Overhead:</td> Trees require additional memory to store node references or pointers, which can result in higher memory usage compared to linear data structures like arrays or lists. </tr><tr><td>Complex Implementation:</td> Implementing and maintaining a tree data structure can be more complex compared to other data structures like arrays or lists, especially for balanced tree variants. </tr><tr><td>Limited Operations:</td> Some tree variants, like binary search trees, do not support efficient operations like finding the kth smallest element or finding the rank of an element. </tr></ol> <p> <strong>Functions:</strong> </p> <ol class="points"> <tr><td>Insertion:</td> Add a new node to the tree. </tr><tr><td>Deletion:</td> Remove a node from the tree. </tr><tr><td>Search:</td> Find a specific node or element in the tree. </tr><tr><td>Traversal:</td> Traverse the tree in different orders, such as in-order, pre-order, or post-order. </tr><tr><td>Height/Depth:</td> Calculate the height or depth of the tree. </tr><tr><td>Balance:</td> Ensure the tree remains balanced to maintain efficient operations. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> TreeExample.java</p> <pre> import java.util.*; class TreeNode { int value; TreeNode left; TreeNode right; public TreeNode(int value) { this.value = value; left = null; right = null; } } public class TreeExample { public static void main(String[] args) { // Create a binary search tree TreeNode root = new TreeNode(50); root.left = new TreeNode(30); root.right = new TreeNode(70); root.left.left = new TreeNode(20); root.left.right = new TreeNode(40); root.right.left = new TreeNode(60); root.right.right = new TreeNode(80); // Perform common operations System.out.println('In-order Traversal:'); inOrderTraversal(root); System.out.println('
Search for value 40: '+search(root, 40)); System.out.println('Search for value 90: '+search(root, 90)); int minValue = findMinValue(root); System.out.println('Minimum value in the tree: '+minValue); int maxValue = findMaxValue(root); System.out.println('Maximum value in the tree: '+maxValue); } // In-order traversal: left subtree, root, right subtree public static void inOrderTraversal(TreeNode node) { if (node != null) { inOrderTraversal(node.left); System.out.print(node.value + ' '); inOrderTraversal(node.right); } } // Search for a value in the tree public static boolean search(TreeNode node, int value) { if (node == null) return false; if (node.value == value) return true; if (value <node.value) return search(node.left, value); else search(node.right, } find the minimum value in tree public static int findminvalue(treenode node) { if (node.left="=" null) node.value; findminvalue(node.left); maximum findmaxvalue(treenode (node.right="=" findmaxvalue(node.right); < pre> <p> <strong>Output:</strong> </p> <pre> In-order Traversal:20 30 40 50 60 70 80 Search for value 40: true Search for value 90: false Minimum value in the tree: 20 Maximum value in the tree: 80 </pre> <hr></node.value)></pre></v;i++)></list></pre></numbers.length;i++)> 2) ArrayList:
ArrayList в Java е динамична структура от данни, която позволява съхранение и манипулиране на елементи. Той е част от Java Collections Framework и е реализиран с помощта на вътрешен масив.
Предимства:
Недостатъци:
Функции:
инструмент за лечение gimp
Изпълнение:
Име на файл: ArrayListExample.java
import java.util.*; public class ArrayListExample { public static void main(String[] args) { // Create an ArrayList to store integers ArrayList numbers=new ArrayList(List.of(10,20,30,40,50)); //Access and print elements from the ArrayList System.out.println('Element at index 0:'+numbers.get(0)); System.out.println('Element at index 2:'+numbers.get(2)); System.out.println('Element at index 4:'+numbers.get(4)); // Calculate and print the sum of all elements in the ArrayList int sum=numbers.stream().mapToInt(Integer::intValue).sum(); System.out.println('Sum of ArrayList elements:'+sum); // Update an element in the ArrayList numbers.set(2,35); System.out.println('Updated element at index 2:'+numbers.get(2)); // Iterate through the ArrayList using a for-each loop and print the elements System.out.println('Elements in the ArrayList:'); for (int number:numbers) { System.out.println(number); } } } Изход:
Element at index 0:10 Element at index 2:30 Element at index 4:50 Sum of ArrayList elements:150 Updated element at index 2:35 Elements in the ArrayList: 10 20 35 40 50
3) Свързан списък:
Свързаният списък е линейна структура от данни, в която елементите се съхраняват в отделни обекти, наречени възли. Референтна връзка към следващия възел в последователността е включена във всеки елемент от данни на възел. Последният възел на списъка се свързва с null, което показва, че списъкът е приключил.
За разлика от масивите, свързаните списъци не изискват непрекъснато разпределение на паметта. Всеки възел в свързан списък може да бъде разпределен независимо, което позволява динамично разпределение на паметта и ефективни операции за вмъкване и изтриване.
равенство на java обекти
Предимства:
Недостатъци:
Функции:
Изпълнение:
Име на файл: LinkedList1.java
import java.util.*; public class LinkedList1 { public static void main(String[] args) { // Create a LinkedList to store integers LinkedList linkedList1 = new LinkedList(); // Add elements to the LinkedList linkedList1.add(10); linkedList1.add(20); linkedList1.add(30); linkedList1.add(40); linkedList1.add(50); // Print the LinkedList System.out.println('LinkedList:'+linkedList1); // Remove an element from the LinkedList linkedList1.removeFirst(); System.out.println('LinkedList after removing first element:'+linkedList1); // Check if an element exists in the LinkedList boolean containsElement=linkedList1.contains(30); System.out.println('LinkedList contains element 30?'+containsElement); // Get the first and last elements of the LinkedList int firstElement=linkedList1.getFirst(); int lastElement=linkedList1.getLast(); System.out.println('First element:'+firstElement); System.out.println('Last element:'+lastElement); // Clear the LinkedList linkedList1.clear(); System.out.println('LinkedList after clearing:'+linkedList1); } } Изход:
LinkedList:[10, 20, 30, 40, 50] LinkedList after removing first element:[20, 30, 40, 50] LinkedList contains element 30?true First element:20 Last element:50 LinkedList after clearing:[]
4) Стек:
Принципът „Последен влязъл, първи излязъл“ (LIFO) диктува, че елементът, който е бил най-скоро вмъкнат, е и елементът, който е премахнат първи. Стекът е линейна структура от данни, която следва това правило. Той използва командите „push“ и „pop“, за да добави елементи към стека и съответно да премахне най-горния елемент от стека. Техниката „надникване“ допълнително позволява достъп до горния елемент, без да го премахвате.
Характеристики на стека:
Предимства:
Недостатъци:
Изпълнение:
Име на файл: StackExample.java
import java.util.Stack; public class StackExample { public static void main(String[] args) { // Create a stack Stack stack=new Stack(); // Push elements onto the stack stack.push(10); stack.push(20); stack.push(30); // Print the top element of the stack System.out.println('Top element:'+stack.peek()); // Pop elements from the stack int poppedElement=stack.pop(); System.out.println('Popped element:'+poppedElement); // Check if the stack is empty System.out.println('Is stack empty?'+stack.isEmpty()); // Get the size of the stack System.out.println('Stack size:'+stack.size()); // Iterate over the stack System.out.println('Stack elements:'); for (Integer element:stack) { System.out.println(element); } } } Изход:
Top element:30 Popped element:30 Is stack empty?false Stack size:2 Stack elements: 10 20
5) Опашка:
Опашката е линейна структура от данни в Java, която следва принципа „първи влязъл, първи излязъл“ (FIFO). Представлява колекция от елементи, където елементите се вмъкват отзад и се отстраняват отпред.
Характеристика:
Предимства:
Недостатъци:
Изпълнение:
Име на файл: QueueExample.java
import java.util.Stack; import java.util.LinkedList; import java.util.Queue; public class QueueExample { public static void main(String[] args) { // Create a Queue to store integers Queue queue=new LinkedList(); // Enqueue elements to the Queue queue.offer(10); queue.offer(20); queue.offer(30); queue.offer(40); queue.offer(50); //Access and print the front element of the Queue System.out.println('Front element:'+queue.peek()); // Dequeue elements from the Queue and print them while (!queue.isEmpty()) { int element=queue.poll(); System.out.println('Dequeued element:'+element); } } } Изход:
Front element:10 Dequeued element:10 Dequeued element:20 Dequeued element:30 Dequeued element:40 Dequeued element:50
6) HashMap:
HashMap е структура от данни в Java, която предоставя начин за съхраняване и извличане на двойки ключ-стойност. Той е част от Java Collections Framework и се изпълнява въз основа на структурата на данните на хеш-таблицата.
Функции:
Предимства:
Недостатъци:
Изпълнение:
Име на файл: HashMapExample.java
import java.util.HashMap; public class HashMapExample { public static void main(String[] args) { // Create a HashMap to store String keys and Integer values HashMap hashMap=new HashMap(); // Add key-value pairs to the HashMap hashMap.put('John',25); hashMap.put('Alice',30); hashMap.put('Bob',35); //Access and print values based on keys System.out.println('Age of John:'+hashMap.get('John')); System.out.println('Age of Alice:'+hashMap.get('Alice')); // Check if a key exists in the HashMap System.out.println('Is Bob present?'+hashMap.containsKey('Bob')); // Update the value associated with a key hashMap.put('Alice',32); // Remove a key-value pair from the HashMap hashMap.remove('John'); // Print all key-value pairs in the HashMap System.out.println('Key-Value pairs in the HashMap:'); for (String key : hashMap.keySet()) { System.out.println(key+':'+hashMap.get(key)); } // Check the size of the HashMap System.out.println('Size of the HashMap:'+hashMap.size()); } } Изход:
Age of John:25 Age of Alice:30 Is Bob present?true Key-Value pairs in the HashMap: Bob:35 Alice:32 Size of the HashMap:2
7) HashSet:
HashSet е структура от данни в Java, която реализира интерфейса Set и съхранява елементи в хеш таблица.
Характеристика:
Предимства:
Недостатъци:
как да стартирате скрипт на linux
Изпълнение:
Име на файл: HashSetExample.java
import java.util.HashSet; public class HashSetExample { public static void main(String[] args) { // Create a HashSet HashSet set=new HashSet(); // Add elements to the HashSet set.add('Apple'); set.add('Banana'); set.add('Orange'); set.add('Grapes'); set.add('Mango'); // Print the HashSet System.out.println('HashSet:'+set); // Check if an element exists System.out.println('Contains 'Apple':'+set.contains('Apple')); // Remove an element set.remove('Banana'); // Print the updated HashSet System.out.println('Updated HashSet:'+set); // Get the size of the HashSet System.out.println('Size of HashSet:'+set.size()); // Clear the HashSet set.clear(); // Check if the HashSet is empty System.out.println('Is HashSet empty?'+set.isEmpty()); } } Изход:
HashSet:[Apple, Grapes, Mango, Orange, Banana] Contains 'Apple':true Updated HashSet:[Apple, Grapes, Mango, Orange] Size of HashSet:4 Is HashSet empty?true
8) TreeSet:
TreeSet е реализация на интерфейса SortedSet в Java, който използва самобалансиращо се двоично дърво за търсене, наречено червено-черно дърво, за съхраняване на елементи в сортиран ред.
Предимства:
Недостатъци:
Функции:
Изпълнение:
сортиране на списък с масиви java
Име на файл: TreeSetExample.java
import java.util.TreeSet; public class TreeSetExample { public static void main(String[] args) { // Create a TreeSet TreeSet numbers=new TreeSet(); // Add elements to the TreeSet numbers.add(5); numbers.add(2); numbers.add(8); numbers.add(1); numbers.add(4); // Print the TreeSet System.out.println('Elements in the TreeSet:'+numbers); // Check if an element exists System.out.println('Does TreeSet contain 4?'+numbers.contains(4)); // Remove an element numbers.remove(2); // Print the TreeSet after removal System.out.println('Elements in the TreeSet after removal:'+numbers); // Get the size of the TreeSet System.out.println('Size of the TreeSet:'+numbers.size()); // Get the first and last element System.out.println('First element:'+numbers.first()); System.out.println('Last element:'+numbers.last()); // Iterate over the TreeSet System.out.println('Iterating over the TreeSet:'); for (int number:numbers) { System.out.println(number); } } } Изход:
Elements in the TreeSet:[1, 2, 4, 5, 8] Does TreeSet contain 4? true Elements in the TreeSet after removal:[1, 4, 5, 8] Size of the TreeSet:4First element:1 Last element:8 Iterating over the TreeSet: 1 4 5 8
9) TreeMap:
TreeMap е клас в Java, който имплементира интерфейса Map и предоставя сортирано съпоставяне на ключ-стойност въз основа на естествения ред на ключовете или потребителски компаратор.
Предимства:
Недостатъци:
Функции:
Изпълнение:
Име на файл: TreeMapExample.java
import java.util.TreeMap; public class TreeMapExample { public static void main(String[] args) { // Create a TreeMap TreeMap scores=new TreeMap(); // Insert key-value pairs into the TreeMap scores.put('Alice',90); scores.put('Bob',80); scores.put('Charlie',95); scores.put('David',87); scores.put('Eve',92); //Access and print values from the TreeMap System.out.println('Score of Alice:'+scores.get('Alice')); System.out.println('Score of Charlie:'+scores.get('Charlie')); System.out.println('Score of David:'+scores.get('David')); // Update a value in the TreeMap scores.put('Bob',85); // Remove a key-value pair from the TreeMap scores.remove('Eve'); // Iterate through the TreeMap using a for-each loop System.out.println('Scores in the TreeMap:'); for (String name:scores.keySet()) { int score=scores.get(name); System.out.println(name+':'+score); } } } Изход:
Score of Alice:90 Score of Charlie:95 Score of David:87 Scores in the TreeMap: Alice:90 Bob:85 Charlie:95 David:87
10) Графика:
Графите са структура от данни, която представлява колекция от взаимосвързани възли или върхове. Те са съставени от върхове и ръбове, където върховете представляват обекти, а ръбовете представляват връзките между тези обекти.
Предимства:
Недостатъци:
Изпълнение:
Име на файл: GraphExample.java
import java.util.*; public class GraphExample { private int V; // Number of vertices private List<list> adjacencyList; // Adjacency list representation public GraphExample(int V) { this.V=V; adjacencyList=new ArrayList(V); // Initialize the adjacency list for (int i=0;i<v;i++) { adjacencylist.add(new arraylist()); } function to add an edge between two vertices public void addedge(int source,int destination) adjacencylist.get(source).add(destination); adjacencylist.get(destination).add(source); perform breadth-first search traversal of the graph bfs(int startvertex) boolean[] visited="new" boolean[v]; queue linkedlist(); visited[startvertex]="true;" queue.add(startvertex); while (!queue.isempty()) int currentvertex="queue.poll();" system.out.print(currentvertex+\' \'); list neighbors="adjacencyList.get(currentVertex);" for (int neighbor:neighbors) if (!visited[neighbor]) visited[neighbor]="true;" queue.add(neighbor); system.out.println(); depth-first dfs(int dfsutil(startvertex,visited); private dfsutil(int vertex,boolean[] visited) visited[vertex]="true;" system.out.print(vertex+\' dfsutil(neighbor,visited); static main(string[] args) v="5;" number graphexample graphexample(v); edges graph.addedge(0,1); graph.addedge(0,2); graph.addedge(1,3); graph.addedge(2,3); graph.addedge(2,4); system.out.print(\'bfs traversal: graph.bfs(0); system.out.print(\'dfs graph.dfs(0); < pre> <p> <strong>Output:</strong> </p> <pre> BFS traversal: 0 1 2 3 4 DFS traversal: 0 1 3 2 4 </pre> <h3>11) Tree:</h3> <p>A tree is a widely used data structure in computer science that represents a hierarchical structure. It consists of nodes connected by edges, where each node can have zero or more child nodes.</p> <p> <strong>Advantages:</strong> </p> <ol class="points"> <tr><td>Hierarchical Structure:</td> Trees provide a natural way to represent hierarchical relationships, such as file systems, organization charts, or HTML/XML documents. </tr><tr><td>Efficient Search:</td> Binary search trees enable efficient searching with a time complexity of O(log n), making them suitable for storing and retrieving sorted data. </tr><tr><td>Fast Insertion and Deletion:</td> Tree data structures offer efficient insertion and deletion operations, especially when balanced, such as AVL trees or Red-Black trees. </tr><tr><td>Ordered Iteration:</td> In-order traversal of a binary search tree gives elements in a sorted order, which is helpful for tasks like printing elements in sorted order or finding the next/previous element. </tr></ol> <p> <strong>Disadvantages:</strong> </p> <ol class="points"> <tr><td>High Memory Overhead:</td> Trees require additional memory to store node references or pointers, which can result in higher memory usage compared to linear data structures like arrays or lists. </tr><tr><td>Complex Implementation:</td> Implementing and maintaining a tree data structure can be more complex compared to other data structures like arrays or lists, especially for balanced tree variants. </tr><tr><td>Limited Operations:</td> Some tree variants, like binary search trees, do not support efficient operations like finding the kth smallest element or finding the rank of an element. </tr></ol> <p> <strong>Functions:</strong> </p> <ol class="points"> <tr><td>Insertion:</td> Add a new node to the tree. </tr><tr><td>Deletion:</td> Remove a node from the tree. </tr><tr><td>Search:</td> Find a specific node or element in the tree. </tr><tr><td>Traversal:</td> Traverse the tree in different orders, such as in-order, pre-order, or post-order. </tr><tr><td>Height/Depth:</td> Calculate the height or depth of the tree. </tr><tr><td>Balance:</td> Ensure the tree remains balanced to maintain efficient operations. </tr></ol> <p> <strong>Implementation:</strong> </p> <p> <strong>FileName:</strong> TreeExample.java</p> <pre> import java.util.*; class TreeNode { int value; TreeNode left; TreeNode right; public TreeNode(int value) { this.value = value; left = null; right = null; } } public class TreeExample { public static void main(String[] args) { // Create a binary search tree TreeNode root = new TreeNode(50); root.left = new TreeNode(30); root.right = new TreeNode(70); root.left.left = new TreeNode(20); root.left.right = new TreeNode(40); root.right.left = new TreeNode(60); root.right.right = new TreeNode(80); // Perform common operations System.out.println('In-order Traversal:'); inOrderTraversal(root); System.out.println('
Search for value 40: '+search(root, 40)); System.out.println('Search for value 90: '+search(root, 90)); int minValue = findMinValue(root); System.out.println('Minimum value in the tree: '+minValue); int maxValue = findMaxValue(root); System.out.println('Maximum value in the tree: '+maxValue); } // In-order traversal: left subtree, root, right subtree public static void inOrderTraversal(TreeNode node) { if (node != null) { inOrderTraversal(node.left); System.out.print(node.value + ' '); inOrderTraversal(node.right); } } // Search for a value in the tree public static boolean search(TreeNode node, int value) { if (node == null) return false; if (node.value == value) return true; if (value <node.value) return search(node.left, value); else search(node.right, } find the minimum value in tree public static int findminvalue(treenode node) { if (node.left="=" null) node.value; findminvalue(node.left); maximum findmaxvalue(treenode (node.right="=" findmaxvalue(node.right); < pre> <p> <strong>Output:</strong> </p> <pre> In-order Traversal:20 30 40 50 60 70 80 Search for value 40: true Search for value 90: false Minimum value in the tree: 20 Maximum value in the tree: 80 </pre> <hr></node.value)></pre></v;i++)></list> 11) Дърво:
Дървото е широко използвана структура от данни в компютърните науки, която представлява йерархична структура. Състои се от възли, свързани с ръбове, като всеки възел може да има нула или повече дъщерни възли.
Предимства:
Недостатъци:
Функции:
Изпълнение:
Име на файл: TreeExample.java
import java.util.*; class TreeNode { int value; TreeNode left; TreeNode right; public TreeNode(int value) { this.value = value; left = null; right = null; } } public class TreeExample { public static void main(String[] args) { // Create a binary search tree TreeNode root = new TreeNode(50); root.left = new TreeNode(30); root.right = new TreeNode(70); root.left.left = new TreeNode(20); root.left.right = new TreeNode(40); root.right.left = new TreeNode(60); root.right.right = new TreeNode(80); // Perform common operations System.out.println('In-order Traversal:'); inOrderTraversal(root); System.out.println('
Search for value 40: '+search(root, 40)); System.out.println('Search for value 90: '+search(root, 90)); int minValue = findMinValue(root); System.out.println('Minimum value in the tree: '+minValue); int maxValue = findMaxValue(root); System.out.println('Maximum value in the tree: '+maxValue); } // In-order traversal: left subtree, root, right subtree public static void inOrderTraversal(TreeNode node) { if (node != null) { inOrderTraversal(node.left); System.out.print(node.value + ' '); inOrderTraversal(node.right); } } // Search for a value in the tree public static boolean search(TreeNode node, int value) { if (node == null) return false; if (node.value == value) return true; if (value <node.value) return search(node.left, value); else search(node.right, } find the minimum value in tree public static int findminvalue(treenode node) { if (node.left="=" null) node.value; findminvalue(node.left); maximum findmaxvalue(treenode (node.right="=" findmaxvalue(node.right); < pre> <p> <strong>Output:</strong> </p> <pre> In-order Traversal:20 30 40 50 60 70 80 Search for value 40: true Search for value 90: false Minimum value in the tree: 20 Maximum value in the tree: 80 </pre> <hr></node.value)> 