- DFA се отнася до детерминистични крайни автомати. Детерминистичното се отнася до уникалността на изчислението. Крайните автомати се наричат детерминистични крайни автомати, ако машината чете входен низ символ по символ.
- В DFA има само един път за конкретен вход от текущото състояние към следващото състояние.
- DFA не приема нулевия ход, т.е. DFA не може да промени състоянието без въведен знак.
- DFA може да съдържа множество крайни състояния. Използва се в лексикален анализ в компилатора.
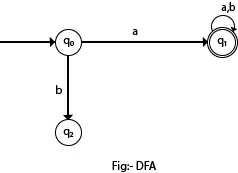
В следващата диаграма можем да видим, че от състояние q0 за вход a има само един път, който отива до q1. По същия начин, от q0, има само един път за вход b, отиващ до q2.
Официално определение на DFA
DFA е колекция от 5-кортежи, както описахме в дефиницията на FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Преходната функция може да се дефинира като:
java listnode
δ: Q x ∑→Q
Графично представяне на DFA
DFA може да бъде представен чрез диграфи, наречени диаграма на състоянието. В който:
- Състоянието е представено от върхове.
- Дъгата, обозначена с въведен знак, показва преходите.
- Първоначалното състояние е отбелязано със стрелка.
- Крайното състояние е означено с двойно кръгче.
Пример 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Решение:
Диаграма на прехода:

Преходна таблица:
| Настоящо състояние | Следващо състояние за вход 0 | Следващо състояние на вход 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Пример 2:
DFA с ∑ = {0, 1} приема всички, започващи с 0.
Решение:

Обяснение:
- В горната диаграма можем да видим, че при даден 0 като вход към DFA в състояние q0, DFA променя състоянието на q1 и винаги преминава към крайно състояние q1 при стартиране на вход 0. Може да приеме 00, 01, 000, 001... .и т.н. Той не може да приеме нито един низ, който започва с 1, защото никога няма да премине в крайно състояние на низ, започващ с 1.
Пример 3:
DFA с ∑ = {0, 1} приема всички, завършващи на 0.
Решение:

Обяснение:
java свързан списък
В горната диаграма можем да видим, че при даден 0 като вход към DFA в състояние q0, DFA променя състоянието на q1. Може да приеме всеки низ, който завършва с 0 като 00, 10, 110, 100....и т.н. Той не може да приеме нито един низ, който завършва с 1, защото никога няма да премине в крайното състояние q1 при 1 вход, така че низът, завършващ с 1, няма да бъде приет или ще бъде отхвърлен.
