Алгоритъмът за вектор на разстоянието е итеративен, асинхронен и разпределен.
Разпространено:Разпределя се така, че всеки възел получава информация от един или повече от своите директно свързани съседи, извършва изчисление и след това разпределя резултата обратно на своите съседи.Итеративно:Той е итеративен, тъй като неговият процес продължава, докато няма повече информация за обмен между съседите.Асинхронен:Не изисква всички негови възли да работят в заключващата стъпка един с друг.
• Алгоритъмът за вектор на разстоянието е динамичен алгоритъм.
• Използва се главно в ARPANET и RIP.
• Всеки рутер поддържа таблица за разстояния, известна като вектор .

Три ключа за разбиране на работата на алгоритъма за векторно маршрутизиране на разстояние:

Познания за цялата мрежа:Всеки рутер споделя знанията си през цялата мрежа. Рутерът изпраща своите събрани знания за мрежата на своите съседи.Маршрутизиране само до съседи:Рутерът изпраща знанията си за мрежата само до онези рутери, които имат директни връзки. Рутерът изпраща всичко, което има за мрежата през портовете. Информацията се получава от рутера и я използва, за да актуализира своята собствена таблица за маршрутизиране.Споделяне на информация на редовни интервали:В рамките на 30 секунди рутерът изпраща информацията до съседните рутери.

Алгоритъм за векторно маршрутизиране на разстояние

Нека d_х(y) е цената на пътя с най-ниска цена от възел x до възел y. Най-малките разходи са свързани с уравнението на Белман-Форд,

 d<sub>x</sub>(y) = min<sub>v</sub>{c(x,v) + d<sub>v</sub>(y)} 

Където minv е уравнението, взето за всички x съседи. След пътуване от x до v, ако разгледаме пътя с най-ниска цена от v до y, цената на пътя ще бъде c(x,v)+d_в(y). Най-малката цена от x до y е минималната от c(x,v)+d_в(y) поема всички съседи.

С алгоритъма за векторно маршрутизиране на разстояние възелът x съдържа следната информация за маршрутизиране:

• За всеки съсед v, цената c(x,v) е цената на пътя от x до директно свързания съсед, v.
• Векторът на разстоянието x, т.е. D_х= [ D_х(y) : y в N ], съдържащ неговата цена до всички дестинации, y, в N.
• Векторът на разстоянието на всеки от неговите съседи, т.е. D_в= [ D_в(y) : y в N ] за всеки съсед v на x.

Маршрутизирането на вектора на разстоянието е асинхронен алгоритъм, при който възел x изпраща копието на своя вектор на разстояние до всички свои съседи. Когато възел x получи новия вектор на разстоянието от един от своите съседни вектори, v, той запазва вектора на разстоянието на v и използва уравнението на Белман-Форд, за да актуализира своя вектор на разстоянието. Уравнението е дадено по-долу:

kmp алгоритъм

 d<sub>x</sub>(y) = min<sub>v</sub>{ c(x,v) + d<sub>v</sub>(y)} for each node y in N 

Възелът x е актуализирал собствената си векторна таблица на разстоянието, като е използвал горното уравнение и изпраща своята актуализирана таблица до всички свои съседи, така че те да могат да актуализират собствените си вектори на разстоянието.

Алгоритъм

 At each node x, <p> <strong>Initialization</strong> </p> for all destinations y in N: D<sub>x</sub>(y) = c(x,y) // If y is not a neighbor then c(x,y) = &#x221E; for each neighbor w D<sub>w</sub>(y) = ? for all destination y in N. for each neighbor w send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to w <strong>loop</strong> <strong>wait</strong> (until I receive any distance vector from some neighbor w) for each y in N: D<sub>x</sub>(y) = minv{c(x,v)+D<sub>v</sub>(y)} If D<sub>x</sub>(y) is changed for any destination y Send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to all neighbors <strong>forever</strong> 

Забележка: В векторния алгоритъм за разстояние възелът x актуализира таблицата си, когато или види някаква промяна на разходите в един директно свързан възел, или получи векторна актуализация от някой съсед.

Нека разберем чрез пример:

Споделяне на информация

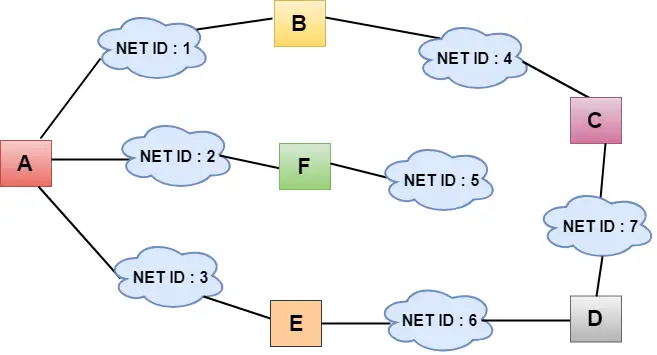
• В горната фигура всеки облак представлява мрежата, а числото вътре в облака представлява идентификатора на мрежата.
• Всички локални мрежи са свързани с рутери и са представени в полета, обозначени като A, B, C, D, E, F.
• Алгоритъмът за векторно маршрутизиране на разстояние опростява процеса на маршрутизиране, като приема, че цената на всяка връзка е една единица. Следователно ефективността на предаването може да бъде измерена чрез броя на връзките за достигане до дестинацията.
• При векторно маршрутизиране на разстояние цената се основава на броя на скокове.

На фигурата по-горе наблюдаваме, че рутерът изпраща знанията до непосредствените съседи. Съседите добавят тези знания към собствените си знания и изпращат актуализираната таблица на собствените си съседи. По този начин рутерите получават собствена информация плюс новата информация за съседите.

Таблица за маршрутизиране

Възникват два процеса:

• Създаване на таблицата
• Актуализиране на таблицата

Създаване на таблицата

Първоначално се създава таблица за маршрутизиране за всеки рутер, която съдържа най-малко три вида информация, като ID на мрежата, цената и следващия хоп.

МРЕЖЕН ИД:Мрежовият идентификатор определя крайната дестинация на пакета.Цена:Цената е броят хопове, които пакетът трябва да измине, за да стигне до там.Следващ скок:Това е рутерът, до който трябва да бъде доставен пакетът.

• На горната фигура са показани оригиналните таблици за маршрутизиране на всички рутери. В таблица за маршрутизиране първата колона представлява идентификатора на мрежата, втората колона представлява цената на връзката, а третата колона е празна.
• Тези таблици за маршрутизиране се изпращат до всички съседи.

Например:

 A sends its routing table to B, F & E. B sends its routing table to A & C. C sends its routing table to B & D. D sends its routing table to E & C. E sends its routing table to A & D. F sends its routing table to A. 

Актуализиране на таблицата

• Когато A получи таблица за маршрутизиране от B, тогава той използва нейната информация, за да актуализира таблицата.
• Таблицата за маршрутизиране на B показва как пакетите могат да се придвижват към мрежи 1 и 4.
• B е съсед на рутера A, пакетите от A до B могат да достигнат в един хоп. И така, 1 се добавя към всички разходи, дадени в таблицата на B, и сумата ще бъде цената за достигане до определена мрежа.

• След корекция A след това комбинира тази таблица със своя собствена таблица, за да създаде комбинирана таблица.

• Комбинираната таблица може да съдържа някои дублирани данни. В горната фигура комбинираната таблица на рутер А съдържа дублиращите се данни, така че запазва само онези данни, които имат най-ниска цена. Например A може да изпрати данните към мрежа 1 по два начина. Първият, който не използва следващ рутер, така че струва един скок. Вторият изисква два скока (A към B, след това B към мрежа 1). Първият вариант е с най-ниска цена, поради което се запазва, а вторият отпада.

• Процесът на създаване на таблицата за маршрутизиране продължава за всички рутери. Всеки рутер получава информацията от съседите и актуализира таблицата за маршрутизиране.

Окончателните таблици за маршрутизиране на всички рутери са дадени по-долу: