Разделяй и владей е алгоритмичен модел. При алгоритмичните методи дизайнът е да се вземе спор за огромен вход, да се раздели входът на незначителни части, да се реши проблемът на всяка от малките части и след това да се слеят решенията на части в глобално решение. Този механизъм за решаване на проблема се нарича стратегия Разделяй и владей.

Алгоритъмът „Разделяй и владей“ се състои от спор, използващ следните три стъпки.

Разделямпървоначалния проблем в набор от подпроблеми.Покори:Решете всеки подпроблем поотделно, рекурсивно.Комбинирайте:Съберете заедно решенията на подпроблемите, за да получите решението на целия проблем.

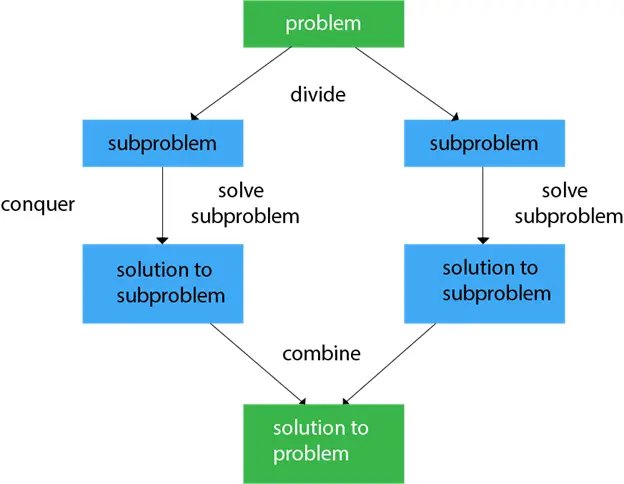
Като цяло можем да следваме разделяй и владей подход в процес от три стъпки.

Примери: Конкретните компютърни алгоритми се основават на подхода Разделяй и владей:

1. Максимален и минимален проблем
2. Двоично търсене
3. Сортиране (сортиране чрез сливане, бързо сортиране)
4. Кулата на Ханой.

Основа на стратегията „Разделяй и владей“:

Има две основни принципи на стратегията 'Разделяй и владей':

1. Релационна формула
2. Състояние на спиране

1. Релационна формула: Това е формулата, която генерираме от дадената техника. След генериране на формула ние прилагаме D&C стратегия, т.е. прекъсваме проблема рекурсивно и решаваме повредените подпроблеми.

2. Условие за спиране: Когато разрешим проблема с помощта на стратегията Разделяй и владей, тогава трябва да знаем колко време трябва да прилагаме Разделяй и владей. Така че условието, при което е необходимо да спрем нашите стъпки на рекурсия на D&C, се нарича Условие за спиране.

Приложения на подхода „Разделяй и владей“:

Следните алгоритми се основават на концепцията за техниката Разделяй и владей:

Двоично търсене:Алгоритъмът за двоично търсене е алгоритъм за търсене, който също се нарича търсене с половин интервал или логаритмично търсене. Той работи, като сравнява целевата стойност със средния елемент, съществуващ в сортиран масив. След извършване на сравнението, ако стойността се различава, тогава половината, която не може да съдържа целта, в крайна сметка ще бъде елиминирана, последвано от продължаване на търсенето на другата половина. Отново ще разгледаме средния елемент и ще го сравним с целевата стойност. Процесът продължава да се повтаря, докато целевата стойност бъде постигната. Ако установим, че другата половина е празна след приключване на търсенето, тогава може да се заключи, че целта не присъства в масива.Бързо сортиране:Това е най-ефективният алгоритъм за сортиране, който е известен също като сортиране чрез разделяне. Започва с избиране на опорна стойност от масив, последвано от разделяне на останалите елементи на масива на два подмасива. Разделянето се прави чрез сравняване на всеки от елементите с основната стойност. Той сравнява дали елементът има по-голяма или по-малка стойност от опорната точка и след това рекурсивно сортира масивите.Сортиране при сливане:Това е алгоритъм за сортиране, който сортира масив, като прави сравнения. Започва с разделяне на масив на подмасив и след това рекурсивно сортира всеки от тях. След като сортирането приключи, той ги обединява обратно.Най-близката двойка точки:Това е проблем на изчислителната геометрия. Този алгоритъм набляга на намирането на най-близката двойка точки в метрично пространство, дадени n точки, така че разстоянието между двойката точки да е минимално.Алгоритъмът на Strassen:Това е алгоритъм за умножение на матрици, който е кръстен на Фолкер Щрасен. Доказано е, че е много по-бърз от традиционния алгоритъм, когато работи върху големи матрици.Алгоритъм на Cooley-Tukey Fast Fourier Transform (FFT):Алгоритъмът за бързо преобразуване на Фурие е кръстен на J. W. Cooley и John Turkey. Той следва подхода „Разделяй и владей“ и налага сложност на O(nlogn).Карацуба алгоритъм за бързо умножение:Това е един от най-бързите алгоритми за умножение на традиционното време, изобретен от Анатолий Карацуба в края на 1960 г. и публикуван през 1962 г. Той умножава две n-цифрени числа по такъв начин, като ги редуцира най-много до едноцифрено.

Предимства на Разделяй и владей

• „Разделяй и владей“ има тенденция да решава успешно един от най-големите проблеми, като кулата на Ханой, математически пъзел. Предизвикателство е да се решават сложни проблеми, за които нямате основна представа, но с помощта на подхода „разделяй и владей“ той намали усилията, тъй като работи върху разделянето на основния проблем на две половини и след това ги решава рекурсивно. Този алгоритъм е много по-бърз от другите алгоритми.
• Той ефективно използва кеш паметта, без да заема много място, защото решава прости подпроблеми в рамките на кеш паметта, вместо да осъществява достъп до по-бавната основна памет.
• Тя е по-умела от тази на другата си техника Brute Force.
• Тъй като тези алгоритми възпрепятстват паралелизма, той не включва никаква модификация и се обработва от системи, включващи паралелна обработка.

Недостатъци на разделяй и владей

• Тъй като повечето от неговите алгоритми са проектирани чрез включване на рекурсия, това налага високо управление на паметта.
• Изричният стек може да използва прекомерно пространството.
• Може дори да се срине системата, ако рекурсията е извършена строго по-голяма от наличния стек в процесора.