• Крайният автомат се използва за разпознаване на модели.
• Машината с краен автомат приема низа от символи като вход и съответно променя състоянието си. Във входа, когато се намери желан символ, тогава се извършва преходът.
• По време на прехода автоматите могат или да преминат към следващото състояние, или да останат в същото състояние.
• FA има две състояния: състояние на приемане или състояние на отхвърляне. Когато входният низ бъде обработен успешно и автоматът достигне крайното си състояние, тогава той ще приеме.

Краен автомат се състои от следното:

Q: краен набор от състояния
∑: краен набор от входни символи
q0: начално състояние
F: крайно състояние
d: Преходна функция

Преходната функция може да се дефинира като

 δ: Q x ∑ →Q 

FA се характеризира по два начина:

1. DFA (крайни автомати)
2. NDFA (недетерминирани крайни автомати)

DFA

DFA означава Детерминистични крайни автомати. Детерминистичното се отнася до уникалността на изчислението. В DFA входният знак преминава само в едно състояние. DFA не приема нулевото движение, което означава, че DFA не може да промени състоянието без въведен знак.

DFA има пет кортежа {Q, ∑, q0, F, δ}

Пример

Вижте пример за детерминистични крайни автомати:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}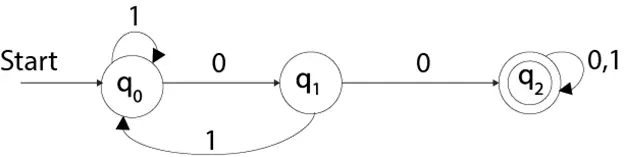 

NDFA

NDFA се отнася до недетерминистичните крайни автомати. Използва се за преминаване през произволен брой състояния за определен вход. NDFA приема движението NULL, което означава, че може да промени състоянието, без да чете символите.

NDFA също има пет състояния, същите като DFA. Но NDFA има различна преходна функция.

Преходната функция на NDFA може да се дефинира като:

Пример

Вижте пример за недетерминистични крайни автомати:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}