Височината или дълбочината на едно двоично дърво може да се определи като максималния или най-големия брой ръбове от листен възел до основния възел или коренов възел до листовия възел. Основният възел ще бъде на ниво нула, което означава, че ако основният възел няма нито един от дъщерните възли, свързани с него, тогава се казва, че височината или дълбочината на конкретното двоично дърво е нула.
Нека вземем пример за по-добро разбиране на височината на двоичното дърво.
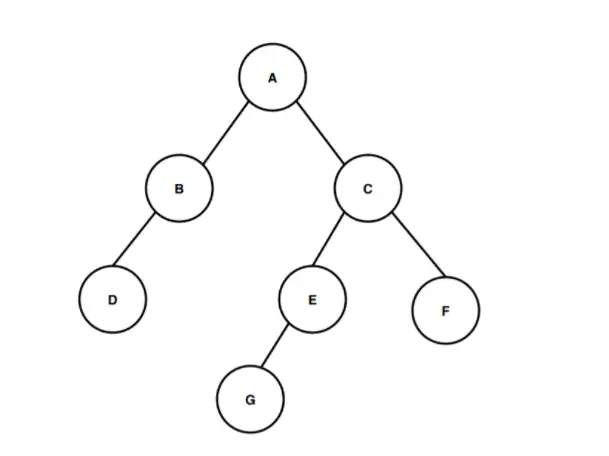
В изображението по-горе имаме двоично дърво, започващо от основния възел с име A. Основният възел A има два дъщерни възела B и C съответно като ляво дете и дясно дете. И по подобен начин ляв дъщерен възел B има само един ляв дъщерен възел, наречен D, а десен дъщерен възел C има два дъщерни възела E и F, от които възел E има възел G като единствено ляво дете.
инстанциране на java
Сега нека изчислим височината на това двоично дърво. Пребройте броя на ръбовете, започващи от коренния възел до най-дълбокия листен възел, за да изчислите височината на двоичното дърво. Най-дълбокият възел, който присъства в това двоично дърво, е възелът G. И така, за изчисляването на височината или дълбочината на това двоично дърво трябва да изчислим броя на ръбовете между основния възел и най-дълбокия възел G. Първият ръб е от възел A до възел C, вторият ръб е от възел C до възел E, а третият ръб е от възел E до възел G. Така че за преминаване от основния възел A до най-дълбокия възел G има три ръба , така че височината или дълбочината на двоичното дърво е 3. Пътят, който следвахме, за да се придвижим от корена до най-дълбокия листен възел, е A > C > E > G и този път покрива три ръба по време на обхождането, ето защо според спрямо дефиницията на височината на двоичното дърво, височината на това двоично дърво е 3.
Начини за намиране на височината на двоичното дърво
Сега нека напишем код за намиране на височината на двоично дърво. Има два начина да намерите височината на двоичното дърво. Единият е рекурсивен метод а другият е нерекурсивен метод който ще използва структурата от данни на Queue, за да изчисли височината на двоичното дърво.
Рекурсивен начин
Първо, нека видим рекурсивния начин за намиране на височината на двоичното дърво.
Код:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Изход: Резултатът от горния код е:
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
По рекурсивен начин извикахме височина() функция многократно, за да намерите височината на двоичното дърво. Основният възел на двоичното дърво се предава като параметър на функцията height(). Функцията height() изчислява височината на двете поддървета на основния възел и коя от двете височини е по-висока, се счита за височина на двоичното дърво.
Нерекурсивен начин
Сега нека видим нерекурсивния начин за намиране на височината на двоичното дърво.
Код:
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> При този подход използвахме нерекурсивен начин за намиране на дълбочината на двоичното дърво. За да намерим височината на двоичното дърво, ние написахме функция с име height, която ще изисква параметър от тип Node (това означава корена на двоичното дърво, чиято височина трябва да бъде изчислена). Коренът на двоичното дърво присъства на ниво нула, което означава, че височината или дълбочината на корена е нула.
При нерекурсивния подход ние използваме структурата на данните на опашката, за да намерим дълбочината на двоичното дърво. Възлите на двоичното дърво, за които искаме да намерим дълбочината, се добавят към структурата от данни на Queue с помощта на операция за поставяне на опашка, на която възелът на двоичното дърво се предава като параметър на тази функция.
linux команди създават папка
След като всички възли са добавени към опашката, възлите, добавени в опашката, се премахват чрез извикване на функцията за премахване на опашката, която ще продължи да премахва един елемент от опашката, докато не бъде открит нулевият възел на двоичното дърво. Всеки път, когато възел на двоичното дърво от опашката бъде премахнат, променливата за дълбочина, представляваща дълбочината на двоичното дърво, се увеличава с единица. И в крайна сметка стойността на променливата за дълбочина ще представлява крайната дълбочина на двоичното дърво.
