Алгоритъмът на Bellman ford е алгоритъм за най-кратък път с един източник. Този алгоритъм се използва за намиране на най-късото разстояние от единичния връх до всички останали върхове на претеглен граф. Има различни други алгоритми, използвани за намиране на най-краткия път, като алгоритъма на Дейкстра и т.н. Ако претеглената графика съдържа отрицателни стойности на теглото, тогава алгоритъмът на Дейкстра не потвърждава дали дава правилния отговор или не. За разлика от алгоритъма на Дейкстра, алгоритъмът на Белман Форд гарантира правилния отговор дори ако претеглената графика съдържа отрицателни стойности на тегло.
Правило на този алгоритъм
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
Разгледайте графиката по-долу:
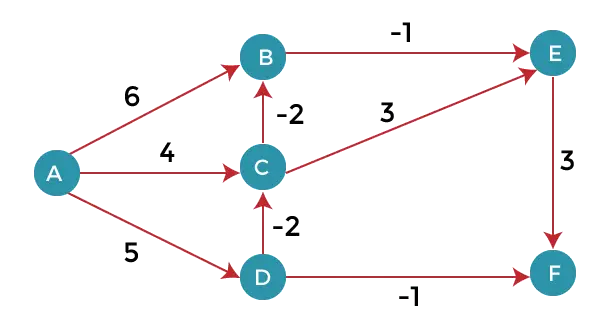
Както можем да видим в горната графика, някои от теглата са отрицателни. Горната графика съдържа 6 върха, така че ще продължим да се отпускаме до 5-те върха. Тук ще отпуснем всички ръбове 5 пъти. Цикълът ще повтори 5 пъти, за да получи правилния отговор. Ако цикълът се повтори повече от 5 пъти, тогава и отговорът ще бъде същият, т.е. няма да има промяна в разстоянието между върховете.
Релаксиращ означава:
linux мента канела срещу мате
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
d(v) = 0 + 6 = 6
Следователно разстоянието на върха B е 6.
Помислете за ръба (A, C). Обозначете върха 'A' като 'u' и върха 'C' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 0
d(v) = ∞
c(u, v) = 4
Тъй като (0 + 4) е по-малко от ∞, актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Следователно разстоянието на върха C е 4.
Помислете за ръба (A, D). Обозначете върха 'A' като 'u' и върха 'D' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 0
d(v) = ∞
c(u, v) = 5
Тъй като (0 + 5) е по-малко от ∞, актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 0 + 5 = 5
Следователно разстоянието на върха D е 5.
Помислете за ръба (B, E). Обозначете върха 'B' като 'u' и върха 'E' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 6
d(v) = ∞
c(u, v) = -1
Тъй като (6 - 1) е по-малко от ∞, така че актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 6 - 1 = 5
Следователно разстоянието на върха E е 5.
Помислете за ръба (C, E). Обозначете върха 'C' като 'u' и върха 'E' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 4
d(v) = 5
c(u, v) = 3
Тъй като (4 + 3) е по-голямо от 5, така че няма да има актуализиране. Стойността във връх E е 5.
Помислете за ръба (D, C). Обозначете върха 'D' като 'u' и върха 'C' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 5
d(v) = 4
c(u, v) = -2
Тъй като (5 -2) е по-малко от 4, така че актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 5 - 2 = 3
Следователно разстоянието на върха C е 3.
Помислете за ръба (D, F). Обозначете върха 'D' като 'u' и върха 'F' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 5
d(v) = ∞
c(u, v) = -1
Тъй като (5 -1) е по-малко от ∞, актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 5 - 1 = 4
Следователно разстоянието на върха F е 4.
Помислете за ръба (E, F). Обозначете върха 'E' като 'u' и върха 'F' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 5
d(v) = ∞
c(u, v) = 3
Тъй като (5 + 3) е по-голямо от 4, няма да има актуализиране на стойността на разстоянието на върха F.
Помислете за ръба (C, B). Обозначете върха 'C' като 'u' и върха 'B' като 'v'. Сега използвайте релаксиращата формула:
състав на връзката
d(u) = 3
d(v) = 6
c(u, v) = -2
Тъй като (3 - 2) е по-малко от 6, така че актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 3 - 2 = 1
Следователно разстоянието на върха B е 1.
Сега първата итерация е завършена. Преминаваме към втората итерация.
Втора итерация:
Във втората итерация отново проверяваме всички ръбове. Първият ръб е (A, B). Тъй като (0 + 6) е по-голямо от 1, така че няма да има актуализиране във върха B.
Следващият ръб е (A, C). Тъй като (0 + 4) е по-голямо от 3, така че няма да има актуализиране във върха C.
Следващият ръб е (A, D). Тъй като (0 + 5) е равно на 5, така че няма да има актуализиране във върха D.
Следващият ръб е (B, E). Тъй като (1 - 1) е равно на 0, което е по-малко от 5, така че актуализирайте:
d(v) = d(u) + c(u, v)
d(E) = d(B) +c(B, E)
= 1 - 1 = 0
Следващият ръб е (C, E). Тъй като (3 + 3) е равно на 6, което е по-голямо от 5, така че няма да има актуализиране във върха E.
Следващият ръб е (D, C). Тъй като (5 - 2) е равно на 3, така че няма да има актуализиране във върха C.
Следващият ръб е (D, F). Тъй като (5 - 1) е равно на 4, така че няма да има актуализиране във върха F.
Следващият ръб е (E, F). Тъй като (5 + 3) е равно на 8, което е по-голямо от 4, така че няма да има актуализиране във върха F.
Следващият ръб е (C, B). Тъй като (3 - 2) е равно на 1`, така че няма да има актуализиране във върха B.

Трета итерация
Ще извършим същите стъпки, както в предишните повторения. Ще забележим, че няма да има актуализиране на разстоянието на върховете.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
Времева сложност
Времевата сложност на алгоритъма на Белман Форд би била O(E|V| - 1).
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
d(v) = 0 + 5 = 5
Следователно разстоянието на връх 3 е 5.
Помислете за ръба (1, 2). Обозначете върха '1' като 'u' и върха '2' като 'v'. Сега използвайте релаксиращата формула:
sts изтегляне
d(u) = 0
d(v) = ∞
c(u, v) = 4
Тъй като (0 + 4) е по-малко от ∞, актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Следователно разстоянието на връх 2 е 4.
Помислете за ръба (3, 2). Обозначете връх '3' като 'u' и връх '2' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 5
d(v) = 4
c(u, v) = 7
Тъй като (5 + 7) е по-голямо от 4, така че няма да има актуализиране във връх 2.
Помислете за ръба (2, 4). Обозначете връх '2' като 'u' и връх '4' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 4
d(v) = ∞
c(u, v) = 7
Тъй като (4 + 7) е равно на 11, което е по-малко от ∞, така че актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 4 + 7 = 11
Следователно разстоянието на връх 4 е 11.
Помислете за ръба (4, 3). Обозначете връх '4' като 'u' и връх '3' като 'v'. Сега използвайте релаксиращата формула:
d(u) = 11
d(v) = 5
c(u, v) = -15
Тъй като (11 - 15) е равно на -4, което е по-малко от 5, така че актуализирайте
d(v) = d(u) + c(u , v)
d(v) = 11 - 15 = -4
Следователно разстоянието на връх 3 е -4.
Сега преминаваме към втората итерация.
Втора итерация
Сега отново ще проверим всички ръбове. Първият ръб е (1, 3). Тъй като (0 + 5) е равно на 5, което е по-голямо от -4, така че няма да има актуализиране във връх 3.
Следващият ръб е (1, 2). Тъй като (0 + 4) е равно на 4, така че няма да има актуализиране във връх 2.
Следващият ръб е (3, 2). Тъй като (-4 + 7) е равно на 3, което е по-малко от 4, така че актуализирайте:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -4 + 7 = 3
Следователно стойността във връх 2 е 3.
Следващият ръб е (2, 4). Тъй като (3+7) е равно на 10, което е по-малко от 11, така че актуализирайте
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 3 + 7 = 10
Следователно стойността във връх 4 е 10.
великандра
Следващият ръб е (4, 3). Тъй като (10 - 15) е равно на -5, което е по-малко от -4, така че актуализирайте:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 10 - 15 = -5
Следователно стойността във връх 3 е -5.
Сега преминаваме към третата итерация.
Трета итерация
Сега отново ще проверим всички ръбове. Първият ръб е (1, 3). Тъй като (0 + 5) е равно на 5, което е по-голямо от -5, така че няма да има актуализиране във връх 3.
Следващият ръб е (1, 2). Тъй като (0 + 4) е равно на 4, което е по-голямо от 3, така че няма да има актуализиране във връх 2.
Следващият ръб е (3, 2). Тъй като (-5 + 7) е равно на 2, което е по-малко от 3, така че актуализирайте:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -5 + 7 = 2
Следователно стойността във връх 2 е 2.
Следващият ръб е (2, 4). Тъй като (2 + 7) е равно на 9, което е по-малко от 10, така че актуализирайте:
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 2 + 7 = 9
Следователно стойността във връх 4 е 9.
Следващият ръб е (4, 3). Тъй като (9 - 15) е равно на -6, което е по-малко от -5, така че актуализирайте:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 9 - 15 = -6
Следователно стойността във връх 3 е -6.

Тъй като графиката съдържа 4 върха, така че според алгоритъма на Белман Форд ще има само 3 итерации. Ако се опитаме да изпълним 4thитерация на графиката, разстоянието на върховете от дадения връх не трябва да се променя. Ако разстоянието варира, това означава, че алгоритъмът на Bellman Ford не дава правилния отговор.
4thповторение
Първият ръб е (1, 3). Тъй като (0 +5) е равно на 5, което е по-голямо от -6, така че няма да има промяна във връх 3.
Следващият ръб е (1, 2). Тъй като (0 + 4) е по-голямо от 2, така че няма да има актуализиране.
Следващият ръб е (3, 2). Тъй като (-6 + 7) е равно на 1, което е по-малко от 3, така че актуализирайте:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -6 + 7 = 1
В този случай стойността на върха се актуализира. И така, заключаваме, че алгоритъмът на Bellman Ford не работи, когато графиката съдържа отрицателен цикъл на тегло.
Следователно стойността във връх 2 е 1.
