Първо ще разберем двоично дърво и двоично дърво за търсене отделно и след това ще разгледаме разликите между двоично дърво и двоично дърво за търсене.
Какво е двоично дърво?
А Двоично дърво е
Двоичното дърво може да бъде представено като:
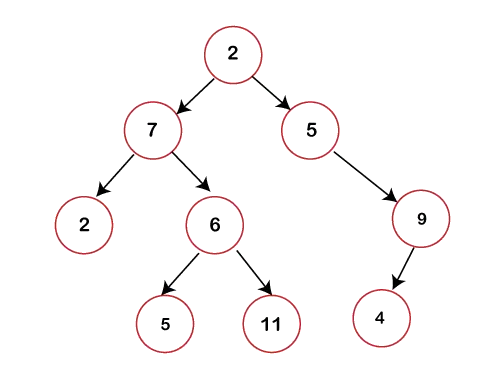
В горната фигура можем да забележим, че всеки възел съдържа най-много 2 деца. Ако някой възел не съдържа ляво или дясно дете, тогава стойността на указателя по отношение на това дете ще бъде NULL.
Основните терминологии, използвани в двоичното дърво, са:
В едно двоично дърво има едно дърво, известно като a перфектно двоично дърво . Това е дърво, в което всички вътрешни възли трябва да съдържат два възела и всички листови възли трябва да са на една и съща дълбочина. В случай на перфектно двоично дърво, общият брой възли, съществуващи в едно двоично дърво, може да бъде изчислен чрез използване на следното уравнение:
n = 2m+1-1
където n е броят на възлите, m е дълбочината на възела.
Какво е двоично дърво за търсене?
А Двоично дърво за търсене е дърво, което следва някакъв ред за подреждане на елементите, докато двоичното дърво не следва никакъв ред. В двоично дърво за търсене стойността на левия възел трябва да е по-малка от родителския възел, а стойността на десния възел трябва да е по-голяма от родителския възел.
Нека разберем концепцията за двоично дърво за търсене чрез примери.

На фигурата по-горе можем да забележим, че стойността на основния възел е 15, което е по-голямо от стойността на всички възли в лявото поддърво. Стойността на коренния възел е по-малка от стойностите на всички възли в дясното поддърво. Сега преминаваме към лявото дете на коренния възел. 10 е по-голямо от 8 и по-малко от 12; то също така удовлетворява свойството на двоичното дърво за търсене. Сега преминаваме към дясното дете на коренния възел; стойността 20 е по-голяма от 17 и по-малка от 25; то също така отговаря на свойството на двоично дърво за търсене. Следователно можем да кажем, че дървото, показано по-горе, е дървото за двоично търсене.
Сега, ако променим стойността от 12 на 16 в горното двоично дърво, трябва да установим дали то все още е дърво за двоично търсене или не.

Стойността на основния възел е 15, което е по-голямо от 10, но по-малко от 16, така че не отговаря на свойството на двоичното дърво за търсене. Следователно, това не е двоично дърво за търсене.
Операции върху двоично дърво за търсене
Можем да извършваме операции за вмъкване, изтриване и търсене в двоичното дърво за търсене. Нека разберем как се извършва търсене при двоично търсене. Двоичното дърво е показано по-долу, върху което трябва да извършим операцията за търсене:

Да предположим, че трябва да търсим 10 в горното двоично дърво. За да извършим двоичното търсене, ще разгледаме всички цели числа в сортиран масив. Първо създаваме пълен списък в пространството за търсене и всички числа ще съществуват в пространството за търсене. Пространството за търсене е маркирано с два указателя, т.е. начало и край. Масивът на горното двоично дърво може да бъде представен като

Първо ще изчислим средния елемент и ще го сравним с елемента, който трябва да се търси. Средният елемент се изчислява с помощта на n/2. Стойността на n е 7; следователно средният елемент е 15. Средният елемент не е равен на търсения елемент, т.е. 10.
Забележка: Ако елементът, който се търси, е по-малък от средния елемент, тогава търсенето ще се извърши в лявата половина; в противен случай търсенето ще се извърши в дясната половина. В случай на равенство елементът се намира.
Тъй като елементът, който ще се търси, е по-малък от средния елемент, така че търсенето ще се извърши в левия масив. Сега търсенето е намалено наполовина, както е показано по-долу:

Средният елемент в левия масив е 10, което е равно на търсения елемент.
Времева сложност
При двоично търсене има n елемента. Ако средният елемент не е равен на търсения елемент, тогава пространството за търсене се намалява до n/2 и ние ще продължим да намаляваме пространството за търсене с n/2, докато не намерим елемента. В цялото намаление, ако преминем от n към n/2 към n/4 и така нататък, тогава ще отнеме log2n стъпки.
Разлики между двоично дърво и двоично дърво за търсене

| База за сравнение | Двоично дърво | Двоично дърво за търсене |
|---|---|---|
| Определение | Двоичното дърво е нелинейна структура от данни, в която възел може да има най-много две деца, т.е. възел може да има 0, 1 или максимум две деца. Двоично дърво за търсене е подредено двоично дърво, в което се следва някакъв ред за организиране на възлите в дърво. | |
| Структура | Структурата на двоичното дърво е, че първият възел или най-горният възел е известен като основен възел. Всеки възел в двоично дърво съдържа левия указател и десния указател. Левият показалец съдържа адреса на лявото поддърво, докато десният показалец съдържа адреса на дясното поддърво. | Двоичното дърво за търсене е един от видовете двоично дърво, което има стойност на всички възли в лявото поддърво, по-малка или равна на коренния възел, а стойността на всички възли в дясно поддърво е по-голяма или равна на стойност на коренния възел. |
| Операции | Операциите, които могат да бъдат реализирани върху двоично дърво, са вмъкване, изтриване и преминаване. | Двоичните дървета за търсене са сортираните двоични дървета, които осигуряват бързо вмъкване, изтриване и търсене. Справките прилагат главно двоично търсене, тъй като всички ключове са подредени в сортиран ред. |
| видове | Четири типа двоични дървета са Пълно двоично дърво, Пълно двоично дърво, Перфектно двоично дърво и Разширено двоично дърво. | Има различни типове двоични дървета за търсене като AVL дървета, Splay дърво, Tango дървета и др. |
