Релационната алгебра е процедурен език за заявки. Той дава стъпка по стъпка процес за получаване на резултата от заявката. Той използва оператори за извършване на заявки.
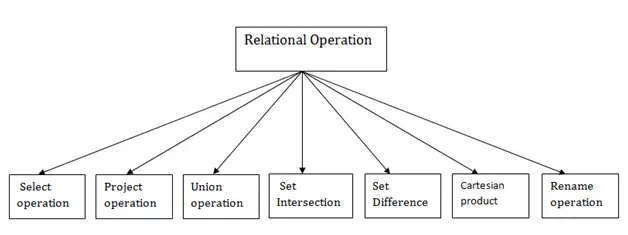
Видове релационни операции
1. Изберете операция:
- Операцията select избира кортежи, които отговарят на даден предикат.
- Означава се със сигма (σ).
Notation: σ p(r)
Където:
стр се използва за прогнозиране на селекцията
r се използва за отношение
стр се използва като пропозиционална логическа формула, която може да използва съединители като: И ИЛИ и НЕ. Тези релационни оператори могат да се използват като релационни оператори като =, ≠, ≧, , ≦.
Например: Заемна връзка
| BRANCH_NAME | LOAN_NO | КОЛИЧЕСТВО |
|---|---|---|
| В центъра | L-17 | 1000 |
| Секвоя | L-23 | 2000 г |
| Перирайд | L-15 | 1500 |
| В центъра | L-14 | 1500 |
| Мианус | L-13 | 500 |
| Раундхълм | L-11 | 900 |
| Перирайд | L-16 | 1300 |
Вход:
σ BRANCH_NAME='perryride' (LOAN)
Изход:
към низ метод java
| BRANCH_NAME | LOAN_NO | КОЛИЧЕСТВО |
|---|---|---|
| Перирайд | L-15 | 1500 |
| Перирайд | L-16 | 1300 |
2. Операция на проекта:
- Тази операция показва списъка с тези атрибути, които искаме да се показват в резултата. Останалите атрибути се елиминират от таблицата.
- Означава се с ∏.
Notation: ∏ A1, A2, An (r)
Където
A1 , A2 , A3 се използва като име на атрибут на релация r .
Пример: ВРЪЗКА С КЛИЕНТА
| ИМЕ | УЛИЦА | ГРАД |
|---|---|---|
| Джоунс | Основен | Харисън |
| Смит | север | ръж |
| Хейс | Основен | Харисън |
| Къри | север | ръж |
| Джонсън | Душа | Бруклин |
| Брукс | Сенатор | Бруклин |
Вход:
∏ NAME, CITY (CUSTOMER)
Изход:
| ИМЕ | ГРАД |
|---|---|
| Джоунс | Харисън |
| Смит | ръж |
| Хейс | Харисън |
| Къри | ръж |
| Джонсън | Бруклин |
| Брукс | Бруклин |
3. Операция на Съюза:
- Да предположим, че има два кортежа R и S. Операцията за обединение съдържа всички кортежи, които са или в R, или в S, или и двете в R & S.
- Той елиминира дублиращите се кортежи. Означава се с ∪.
Notation: R ∪ S
Операцията на обединение трябва да отговаря на следното условие:
- R и S трябва да имат атрибут на едно и също число.
- Дублиращите се кортежи се елиминират автоматично.
Пример:
ВРЪЗКА С ВЛОЖИТЕЛ
| ПОТРЕБИТЕЛСКО ИМЕ | ACCOUNT_NO |
|---|---|
| Джонсън | А-101 |
| Смит | А-121 |
| Майес | А-321 |
| Търнър | А-176 |
| Джонсън | А-273 |
| Джоунс | А-472 |
| Линдзи | А-284 |
ЗАЕМНО ОТНОШЕНИЕ
списък за сортиране на java
| ПОТРЕБИТЕЛСКО ИМЕ | LOAN_NO |
|---|---|
| Джоунс | L-17 |
| Смит | L-23 |
| Хейс | L-15 |
| Джаксън | L-14 |
| Къри | L-93 |
| Смит | L-11 |
| Уилямс | L-17 |
Вход:
конвертиране на низ в int
∏ CUSTOMER_NAME (BORROW) ∪ ∏ CUSTOMER_NAME (DEPOSITOR)
Изход:
| ПОТРЕБИТЕЛСКО ИМЕ |
|---|
| Джонсън |
| Смит |
| Хейс |
| Търнър |
| Джоунс |
| Линдзи |
| Джаксън |
| Къри |
| Уилямс |
| Майес |
4. Задайте пресичане:
- Да предположим, че има два кортежа R и S. Операцията за пресичане на множество съдържа всички кортежи, които са и в R & S.
- Означава се с пресичане ∩.
Notation: R ∩ S
Пример: Използвайки горната таблица DEPOSITOR и таблица BORROW
Вход:
∏ CUSTOMER_NAME (BORROW) ∩ ∏ CUSTOMER_NAME (DEPOSITOR)
Изход:
| ПОТРЕБИТЕЛСКО ИМЕ |
|---|
| Смит |
| Джоунс |
5. Задаване на разлика:
- Да предположим, че има два кортежа R и S. Операцията за пресичане на множество съдържа всички кортежи, които са в R, но не и в S.
- Означава се с пресечна точка минус (-).
Notation: R - S
Пример: Използвайки горната таблица DEPOSITOR и таблица BORROW
Вход:
∏ CUSTOMER_NAME (BORROW) - ∏ CUSTOMER_NAME (DEPOSITOR)
Изход:
| ПОТРЕБИТЕЛСКО ИМЕ |
|---|
| Джаксън |
| Хейс |
| Уилямс |
| Къри |
6. Декартово произведение
- Декартовият продукт се използва за комбиниране на всеки ред в една таблица с всеки ред в другата таблица. Известен е също като кръстосано произведение.
- Означава се с X.
Notation: E X D
Пример:
СЛУЖИТЕЛ
| EMP_ID | EMP_NAME | EMP_DEPT |
|---|---|---|
| 1 | Смит | А |
| 2 | Хари | ° С |
| 3 | Джон | Б |
ОТДЕЛЕНИЕ
| DEPT_NO | DEPT_NAME |
|---|---|
| А | Маркетинг |
| Б | Продажби |
| ° С | Законни |
Вход:
EMPLOYEE X DEPARTMENT
Изход:
| EMP_ID | EMP_NAME | EMP_DEPT | DEPT_NO | DEPT_NAME |
|---|---|---|---|---|
| 1 | Смит | А | А | Маркетинг |
| 1 | Смит | А | Б | Продажби |
| 1 | Смит | А | ° С | Законни |
| 2 | Хари | ° С | А | Маркетинг |
| 2 | Хари | ° С | Б | Продажби |
| 2 | Хари | ° С | ° С | Законни |
| 3 | Джон | Б | А | Маркетинг |
| 3 | Джон | Б | Б | Продажби |
| 3 | Джон | Б | ° С | Законни |
7. Операция за преименуване:
Операцията за преименуване се използва за преименуване на изходната релация. Означава се с ро (p).
азбука с цифри
Пример: Можем да използваме оператора за преименуване, за да преименуваме връзката STUDENT на STUDENT1.
ρ(STUDENT1, STUDENT)
